手把手带你实现二叉树（C/C++ 数据结构）

2026年 02月 09日

简体中文

数据结构笔记4 / 5

上一篇手把手带你实现栈和队列（C/C++ 数据结构）下一篇手把手带你实现图结构（C/C++ 数据结构）

一、引言

在我们之前学过的链表中，每个节点都包含一个数据元素和一个指向下一个节点的指针。他们在内存中是非连续的，但节点之间通过指针连接起来形成一个链式结构。

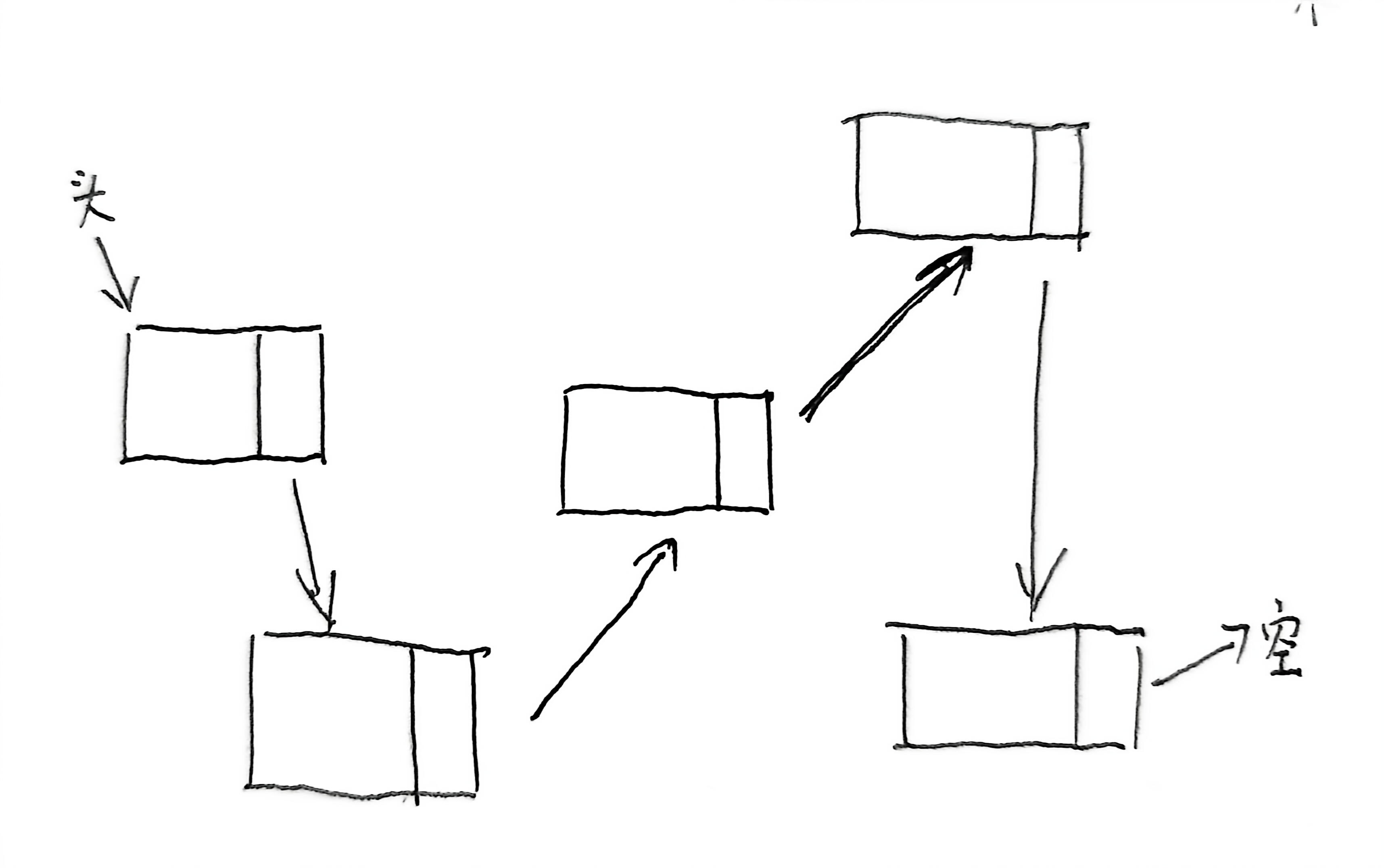
1、什么是二叉树？

而二叉树物理实现也离不开链表,每个节点最多有两个子节点，分别称为左子节点和右子节点。

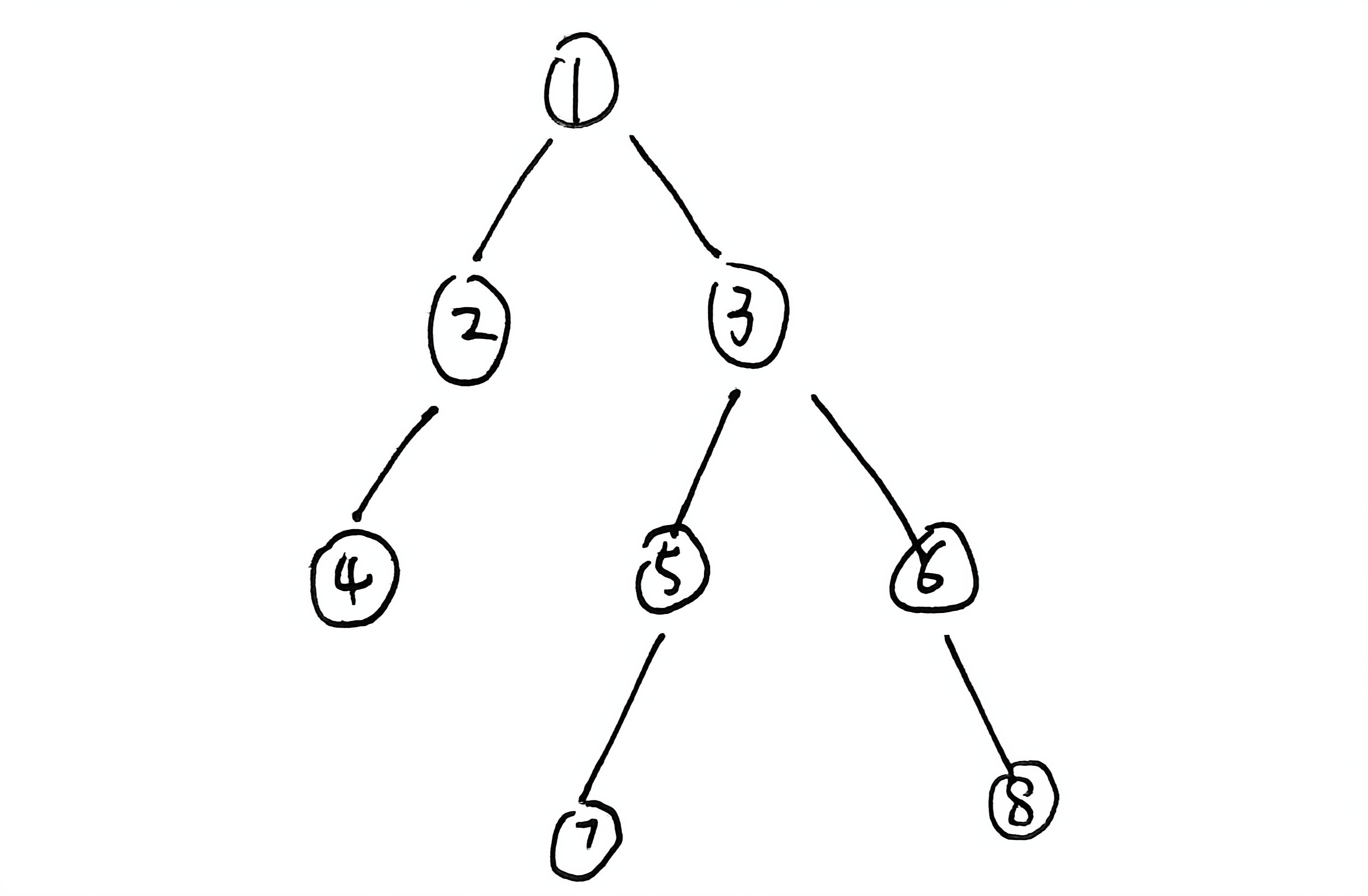
如上图：

根节点（Root）：树的顶端节点，没有父节点。在上图中，节点 1 是根节点。
子节点（Child）：节点的直接后代。在上图中，节点 2 和节点 3 是节点 1 的子节点。
父节点（Parent）：节点的直接前辈。在上图中，节点 1 是节点 2 和节点 3 的父节点。节点 2 是节点 4 的父节点，节点 3 是节点 5 和节点 6 的父节点。
叶子节点（Leaf）：没有子节点的节点。在上图中，节点 4、7、8 是叶子节点。
子树（Subtree）：树的任意节点及其所有后代构成的树。在上图中，节点 2 和节点 3 以及他们的子节点分别构成了两个子树，叫作节点 1 的左子树和右子树。
层（Level）：节点所在的层数，根节点所在的层为 1。在上图中，节点 1 在第 1 层，节点 2 和节点 3 在第 2 层，依次类推。
高度（Height）：树中节点的最大层数。在上图中，最大层数是 4，所以树的高度为 4。

二叉树的结构可以适合用于表示层次关系的数据，如组织结构图、文件系统等。它也被广泛应用于各种算法和数据结构中，如二叉搜索树、堆、哈夫曼树等。

2、为什么要有二叉树？

很简单，因为在某些场景下，二叉树更高效。

比如，现在有一个有序数组 [1, 2, 3, 4, 5, 6, 7]，想知道其中是否存在数字 5。

如果用数组来存储，最坏情况下需要遍历整个数组，时间复杂度为 O(n)。

bool searchArray(vector<int>& arr, int target) {
    for (int num : arr) {
        if (num == target) {
            return true;
        }
    }
    return false;
}

如果用二叉树来存储这个有序数组，我们可以构建一个平衡二叉搜索树（BST），这样在最坏情况下的时间复杂度可以降低到 O(log n)。

        4
      /   \
     2     6
    / \   / \
   1   3 5   7

查找数字5的过程：

1、从根节点4开始：5 > 4 → 向右子树（节点6）查找；

2、到节点6：5 < 6 → 向左子树（节点5）查找；

3、到节点5：5 == 5 → 找到，返回True。

为什么是 O(log n) 呢？因为每次比较后，我们都将搜索范围缩小了一半。

平衡二叉树的高度大约是 log2(n)，因此最多需要比较 log2(n) 次就能找到目标元素。

比如说，如果有 1024 个元素，构建成一个平衡二叉搜索树后，最多需要比较 10 次（因为 2^10 = 1024）就能找到目标元素。相比之下，使用数组需要最多 1024 次比较才能找到目标元素。

二、二叉树的实现

1、二叉树节点

在 C++ 中，我们可以定义一个二叉树节点如下：

class TreeNode {
public:
    int val_; // 节点的值
    TreeNode* left_; // 指向左子节点的指针
    TreeNode* right_; // 指向右子节点的指针

    TreeNode(int x) : val_(x), left_(nullptr), right_(nullptr) {}
};

然后我们就可以创建一些节点，并将它们连接起来形成一棵二叉树：

        4
      /   \
     2     6
    / \   / \
   1   3 5   7

TreeNode* root = new TreeNode(4);
root->left_ = new TreeNode(2);
root->right_ = new TreeNode(6);
root->left_->left_ = new TreeNode(1);
root->left_->right_ = new TreeNode(3);
root->right_->left_ = new TreeNode(5);
root->right_->right_ = new TreeNode(7);

2、二叉树的先序创建

上面的方法虽然可以创建二叉树，但不够灵活。我就想输入一堆数字，自动帮我创建二叉树。

但是一堆数字之间总要有一个规律，才能知道哪个数字是根节点，哪个数字是左子树，哪个数字是右子树。

这里介绍一些规律：

一个二叉树节点有左子树、根节点、右子树三部分组成，如果要把这个二叉树拉平成一个一维的数组，那么就会有三种不同的排列方式：

我们规定左子树始终在右子树的前面

根节点在最前面（根-左-右）：根节点 + 左子树 + 右子树
根节点在中间（左-根-右）：左子树 + 根节点 + 右子树
根节点在最后面（左-右-根）：左子树 + 右子树 + 根节点

比如说上面这棵二叉树：

        4
      /   \
     2     6
    / \   / \
   1   3 5   7

对于每一个节点，都先访问根节点也就是它自己，然后访问它的左子树，最后访问它的右子树，这就是根-左-右的顺序。

对于（4），先访问根节点（4）,再访问它的左子树（2, 1, 3）， 「4」
对于（2, 1, 3），访问根节点（2）,再访问它的左子树（1），「4 2」
对于（1），先访问它自己（1），再访问它的左子树（空），最后访问它的右子树（空）。 「4 2 1」
对于（2, 1, 3），左子树访问完了，接下来访问右子树（3），「4 2 1」
对于（3），先访问它自己（3），再访问它的左子树（空），最后访问它的右子树（空）。 「4 2 1 3」
对于（4），左子树访问完了，接下来访问右子树（6, 5, 7），「4 2 1 3」
对于（6, 5, 7），先访问根节点（6）,再访问它的左子树（5），「4 2 1 3 6」
对于（5），先访问它自己（5），再访问它的左子树（空），最后访问它的右子树（空）。 「4 2 1 3 6 5」
对于（6, 5, 7），左子树访问完了，接下来访问右子树（7），「4 2 1 3 6 5」
对于（7），先访问它自己（7），再访问它的左子树（空），最后访问它的右子树（空）。 「4 2 1 3 6 5 7」

所以根-左-右的顺序就是 「4 2 1 3 6 5 7」

但是根据 4 2 1 3 6 5 7 这串数字，并且知道这是根-左-右的顺序，我们是无法还原出原来的二叉树的。

因为不知道某个节点什么时候是左子树的最后一个节点，什么时候是右子树的第一个节点。

所以我们需要一个特殊的标记来区分左右子树，比如说 0，当我们遇到 0 的时候，就知道左子树已经访问完了，接下来访问的就是右子树。

那么对于上面这棵二叉树，根-左-右的顺序就变成了 「4 2 1 0 0 3 0 0 6 5 0 0 7 0 0」

根据先序的规律来实现二叉树的创建：

class TreeNode {
public:
    int val_;
    TreeNode* left_;
    TreeNode* right_;

    TreeNode(int x) : val_(x), left_(nullptr), right_(nullptr) {}
};

TreeNode* arrayToTree(vector<int>& arr) {
    // 递归终止条件1：数组为空，返回空节点
    if (arr.empty()) {
        return nullptr;
    }

    // 取出数组第一个元素作为当前节点值，并从数组中移除（关键操作）
    int val = arr[0];
    arr.erase(arr.begin()); // 移除第一个元素，后续递归用剩下的数组

    // 递归终止条件2：值为0，代表空节点，直接返回nullptr
    if (val == 0) {
        return nullptr;
    }

    // 1. 创建当前节点
    TreeNode* node = new TreeNode(val);
    // 2. 递归构建左子树（此时数组已移除当前节点值，剩下的先给左子树用）
    node->left_ = arrayToTree(arr);
    // 3. 递归构建右子树（左子树构建完后，剩下的数组给右子树用）
    node->right_ = arrayToTree(arr);

    return node;
}

int main() {
    vector<int> arr = {4, 2, 1, 0, 0, 3, 0, 0, 6, 5, 0, 0, 7, 0, 0};
    TreeNode* root = arrayToTree(arr);
    // 此时 root 就是原来二叉树的根节点
    return 0;
}

步骤	操作	数组变化	节点构建情况
1	取第一个值 4，删除	[2,1,0,0,3,0,0,6,5,0,0,7,0,0]	创建根节点 4，准备构建其左子树
2	取第一个值 2，删除	[1,0,0,3,0,0,6,5,0,0,7,0,0]	创建 4 的左子节点 2，准备构建 2 的左子树
3	取第一个值 1，删除	[0,0,3,0,0,6,5,0,0,7,0,0]	创建 2 的左子节点 1，准备构建 1 的左子树
4	取第一个值 0，删除	[0,3,0,0,6,5,0,0,7,0,0]	1 的左子节点为空，返回 nullptr
5	取第一个值 0，删除	[3,0,0,6,5,0,0,7,0,0]	1 的右子节点为空，返回 nullptr → 1 的左右子树构建完成
6	取第一个值 3，删除	[0,0,6,5,0,0,7,0,0]	创建 2 的右子节点 3，准备构建 3 的左子树
7	取第一个值 0，删除	[0,6,5,0,0,7,0,0]	3 的左子节点为空
8	取第一个值 0，删除	[6,5,0,0,7,0,0]	3 的右子节点为空 → 3 的左右子树完成 → 2 的左右子树完成
9	取第一个值 6，删除	[5,0,0,7,0,0]	创建 4 的右子节点 6，准备构建 6 的左子树
10	取第一个值 5，删除	[0,0,7,0,0]	创建 6 的左子节点 5，左右子树都是 0 → 5 构建完成
11	取第一个值 7，删除	[0,0]	创建 6 的右子节点 7，左右子树都是 0 → 7 构建完成 → 6 构建完成 → 整棵树构建完成

这里需要注意：arr.erase(arr.begin()) 会修改原数组，所以每次递归用的都是 “剩余的数组”，这是前序构建的关键。

3、先序创建的优化版本

上面这个版本虽然能实现二叉树的创建，但效率不高，

因为每次调用 arr.erase(arr.begin()) 都会导致数组元素的移动，时间复杂度为 O(n)。

那如果构建一个节点为 n 的二叉树，整体时间复杂度就会达到 O(n^2)。

优化后的版本，我们可以使用一个全局变量 index 来记录当前访问到数组的哪个位置，这样就不需要每次都删除数组元素了。

class TreeNode {
public:
    int val_;
    TreeNode* left_;
    TreeNode* right_;

    TreeNode(int x) : val_(x), left_(nullptr), right_(nullptr) {}
};

// 优化版：用索引代替erase，不修改原数组，效率更高
TreeNode* arrayToTreeOpt(const vector<int>& arr, int& index) {
    // 递归终止：索引越界 或 当前值为0（空节点）
    if (index >= arr.size() || arr[index] == 0) {
        index++; // 索引后移，处理下一个元素
        return nullptr;
    }

    // 1. 取当前索引的值创建节点
    int val = arr[index];
    index++; // 索引后移，准备处理左子树
    TreeNode* node = new TreeNode(val);

    // 2. 递归构建左子树（索引会在递归中自动后移）
    node->left_ = arrayToTreeOpt(arr, index);
    // 3. 递归构建右子树
    node->right_ = arrayToTreeOpt(arr, index);

    return node;
}

int main() {
    vector<int> arr = {4, 2, 1, 0, 0, 3, 0, 0, 6, 5, 0, 0, 7, 0, 0};
    int index = 0; // 初始索引
    TreeNode* root = arrayToTreeOpt(arr, index);
    return 0;
}

三、二叉树的遍历

1、前序/中序/后序遍历（DFS）

刚才我们介绍了先序创建二叉树的规律，根-左-右的顺序就是前序遍历（Preorder Traversal）的顺序。

直接复刻上面先序创建二叉树的规律，就能实现前序遍历：

void preorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 1. 访问根节点
    cout << root->val_ << " ";
    // 2. 递归访问左子树
    preorderTraversal(root->left_);
    // 3. 递归访问右子树
    preorderTraversal(root->right_);
}

那么中序遍历（Inorder Traversal）的顺序是左-根-右，后序遍历（Postorder Traversal）的顺序是左-右-根。

void inorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 1. 递归访问左子树
    inorderTraversal(root->left_);
    // 2. 访问根节点
    cout << root->val_ << " ";
    // 3. 递归访问右子树
    inorderTraversal(root->right_);
}

void postorderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 1. 递归访问左子树
    postorderTraversal(root->left_);
    // 2. 递归访问右子树
    postorderTraversal(root->right_);
    // 3. 访问根节点
    cout << root->val_ << " ";
}

这种遍历方法叫作递归遍历，也叫深度优先遍历（DFS），或者叫作深度优先搜索（Depth-First Search）。

因为它会一直沿着树的一个分支往下走，直到遇到叶子节点或者空节点才会回退到上一个节点继续访问另一个分支。

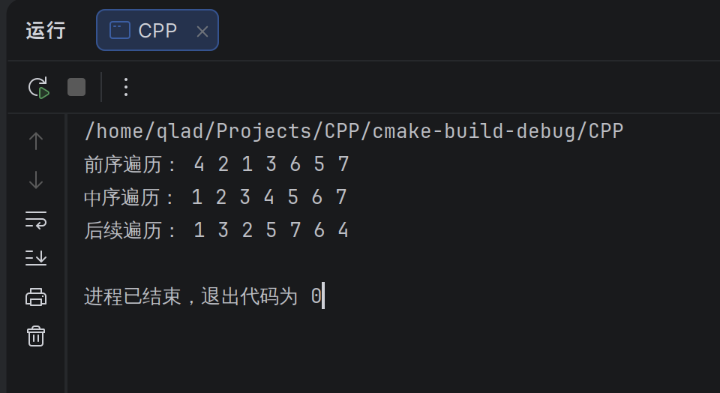
可以发现我们只是修改了几行代码的顺序，就得到了三种不同的遍历方式。所以重要的是理解三个代码位置的含义，而不是死记代码。

另外我们可以采用画图连线的方式来口算前序/中序/后序遍历的结果：

拿上面这棵二叉树来说：

        4
      /   \
     2     6
    / \   / \
   1   3 5   7

口算前序遍历，就把每个节点的左边做个标记，然后从根节点开始，依次连接整个树，然后你的标记点的顺序就是前序遍历的结果：

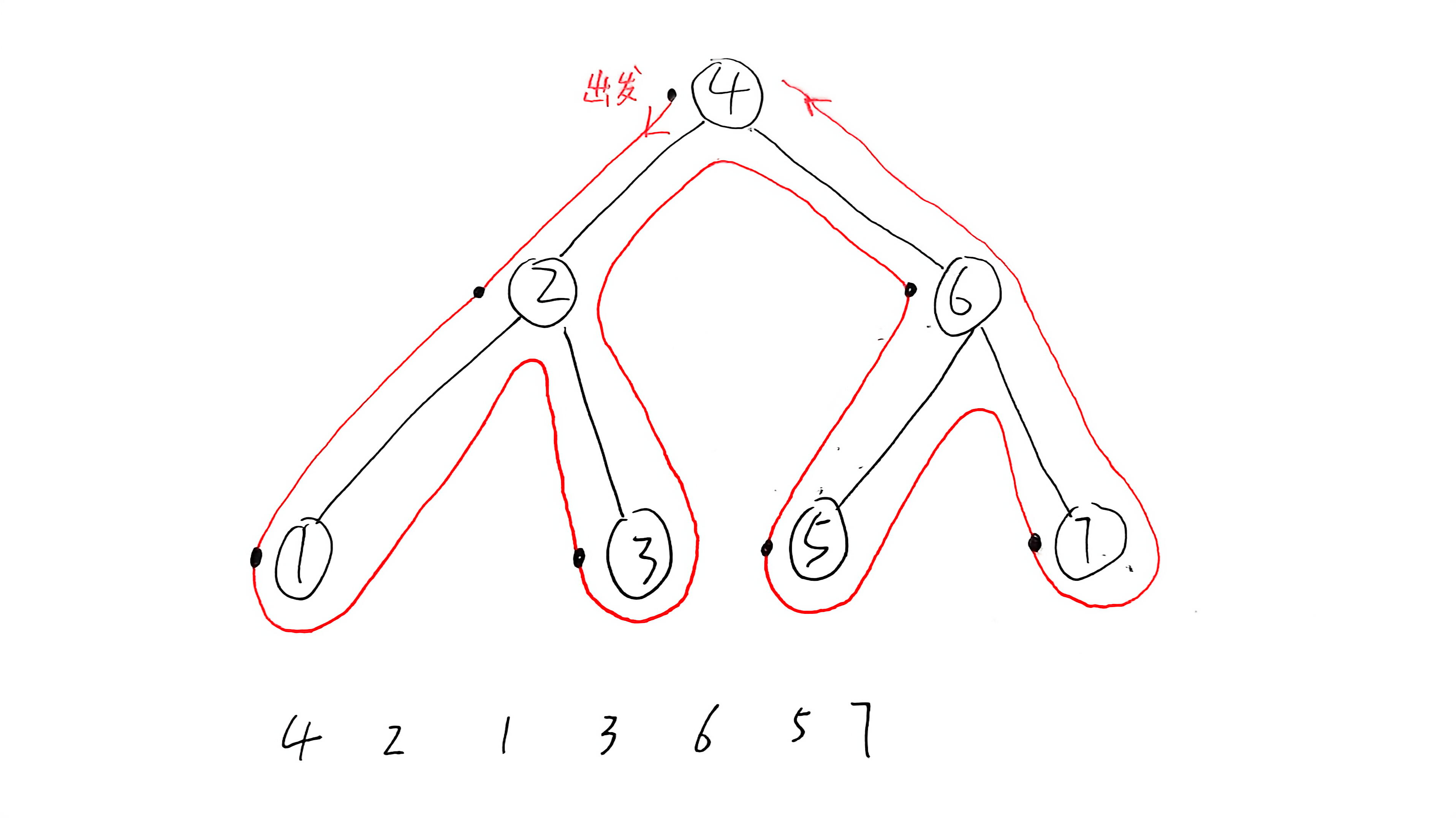
剩下的中序遍历和后序遍历也是同样的方法，中序遍历的标记点在节点的正下方，后序遍历的标记点在节点的右边：

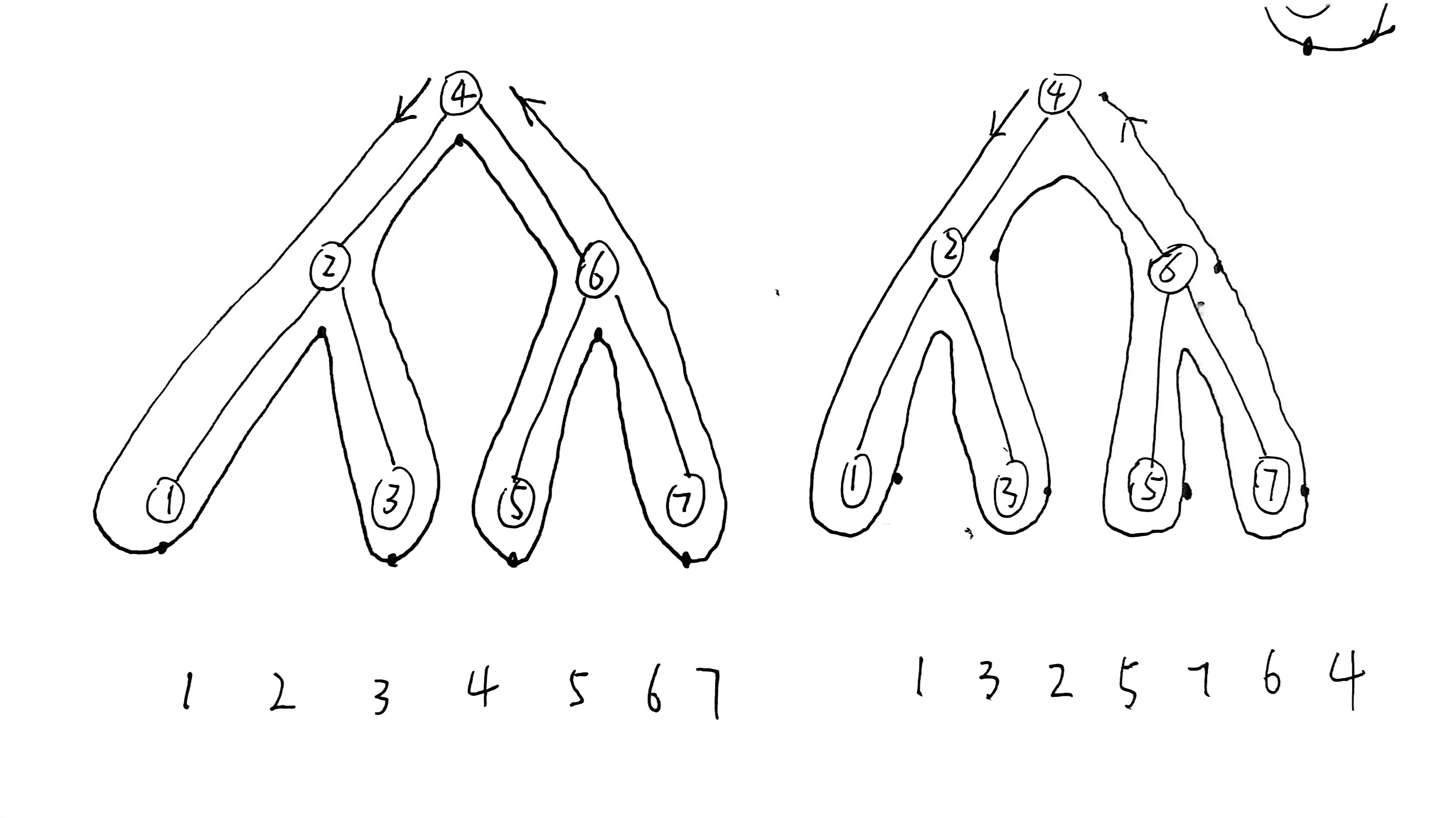
2、层序遍历（BFS）

层序遍历（Level Order Traversal）又叫作广度优先遍历（Breadth-First Search），它的访问顺序是按照树的层级来访问的。

上面的 DFS 是从左向右访问树的每个分支，而 BFS 是从上到下、从左到右访问树的每一层。

void levelOrderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }

    /*
            4
          /   \
         2     6
        / \   / \
       1   3 5   7

    1、使用一个队列来辅助实现。首先将根节点入队，此时队列中只有一个节点：4。
    2、进入循环，队列不为空，取出队首节点4并输出。然后将4的左子节点2和右子节点6入队。此时队列中有两个节点：2, 6。
    3、继续循环，取出队首节点2并输出。然后将2的左子节点1和右子节点3入队。此时队列中有三个节点：6, 1, 3。
    4、继续循环，取出队首节点6并输出。然后将6的左子节点5和右子节点7入队。此时队列中有四个节点：1, 3, 5, 7。
    5、继续循环，取出队首节点1并输出。1没有子节点，所以不入队。 此时队列中有三个节点：3, 5, 7。
    6、继续循环，取出队首节点3并输出。3没有子节点，所以不入队。 此时队列中有两个节点：5, 7。
    7、继续循环，取出队首节点5并输出。5没有子节点，所以不入队。 此时队列中有一个节点：7。
    8、继续循环，取出队首节点7并输出。7没有子节点，所以不入队。 此时队列为空，循环结束。
    */

    queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* cur = q.front();
        q.pop();
        cout << cur->val_ << " ";

        if (cur->left_ != nullptr) {
            q.push(cur->left_);
        }

        if (cur->right_ != nullptr) {
            q.push(cur->right_);
        }
    }
}

对于上述代码进行优化，我们可以输出层数和每层的节点数：

void levelOrderTraversal(TreeNode* root) {
    if (root == nullptr) {
        return;
    }

    queue<TreeNode*> q;
    q.push(root);
    int level = 0; // 记录当前层数
    while (!q.empty()) {
        int size = q.size(); // 当前层的节点数
        cout << "Level " << level << ": ";
        for (int i = 0; i < size; i++) {
            TreeNode* cur = q.front();
            q.pop();
            cout << cur->val_ << " ";

            if (cur->left_ != nullptr) {
                q.push(cur->left_);
            }

            if (cur->right_ != nullptr) {
                q.push(cur->right_);
            }
        }
        cout << endl; // 换行输出下一层
        level++; // 层数加1
    }
}

对比结果如下：

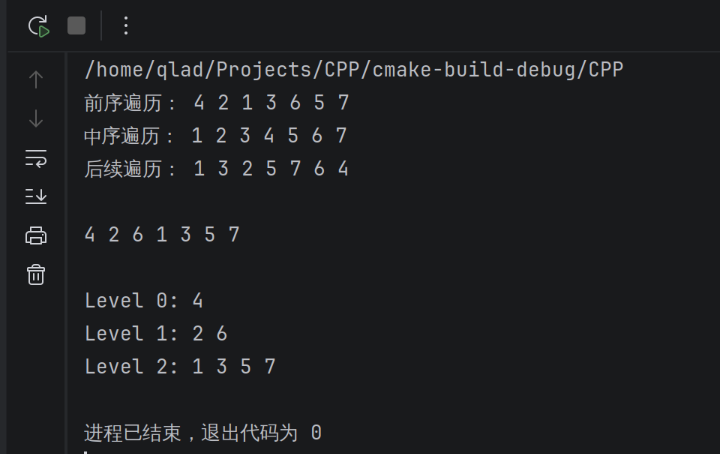
这里将根节点视为第 0 层，有的教材会将根节点视为第 1 层，都可以。

3、DFS 和 BFS 的应用场景

在实际的算法问题中，DFS 算法常用来穷举所有路径，BFS 算法常用来寻找最短路径

拿二叉树的最小深度（Minimum Depth of Binary Tree）这个问题来说：

举个例子：

           1
         /   \
        2     3
       / \   / \
      4   5 6   7
     /   /   \   \
    8   9     10  11
   /     \     \    \
  12     13    14   15
 /              \
16              17

对于这个二叉树来说，最小深度是 5，因为根节点到最近的叶子节点（13/15）的路径包含 5 个节点

用 DFS 也就是递归，对于每一个非叶子节点，我们只用计算左右子树的深度，最后递归下去得到了叶子节点的深度，你就可以比较出最小的那个了。

int minDepth(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    // 如果左子树为空，递归计算右子树的深度
    if (root->left_ == nullptr) {
        return minDepth(root->right_) + 1;
    }
    // 如果右子树为空，递归计算左子树的深度
    if (root->right_ == nullptr) {
        return minDepth(root->left_) + 1;
    }
    // 如果左右子树都不为空，返回较小的深度加1
    return min(minDepth(root->left_), minDepth(root->right_)) + 1;
}

关键节点	子树情况	深度计算结果
16/13/17/15	叶子节点	1
12/14	单侧子树	2
8/10	单侧子树	3
4/6	单侧子树	4
2	双侧（左 4 / 右 3）	min(4,3)+1 = 4
3	双侧（左 4 / 右 3）	min(4,3)+1 = 4
1（根）	双侧（左 4 / 右 4）	min(4,4)+1 = 5

时间复杂度为 O(n)，因为在最坏情况下我们需要访问每个节点一次。

如果用 BFS 来做，我们可以在遍历的过程中记录当前节点的深度，一旦遇到第一个叶子节点，就可以直接返回当前深度了。

int minDepth(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    queue<pair<TreeNode*, int>> q; // 队列中存储节点和对应的深度
    q.push({root, 1}); // 根节点的深度为1
    while (!q.empty()) {
        pair<TreeNode*, int> cur = q.front();
        TreeNode* node = cur.first;
        int depth = cur.second;
        q.pop();
        // 如果当前节点是叶子节点，直接返回当前深度
        if (node->left_ == nullptr && node->right_ == nullptr) {
            return depth;
        }
        // 如果左子节点不为空，入队并记录深度
        if (node->left_ != nullptr) {
            q.push({node->left_, depth + 1});
        }
        // 如果右子节点不为空，入队并记录深度
        if (node->right_ != nullptr) {
            q.push({node->right_, depth + 1});
        }
    }

    return 0; // 这行代码理论上不会被执行到，因为树至少有一个节点（根节点）
}