手把手带你实现栈和队列（C/C++ 数据结构）

2026年 02月 09日

简体中文

上一篇手把手带你实现单/双链表（C/C++ 数据结构）下一篇手把手带你实现二叉树（C/C++ 数据结构）

一、回顾数组和链表

数组和链表都可以在任意位置进行增加和删除操作，拿 vector 和 list 来说：

#include <iostream>
#include <vector>
#include <list>

int main() {
    std::vector<int> vec = {1, 2, 3};
    vec.insert(vec.begin() + 1, 4); // 在索引1位置插入4
    vec.erase(vec.begin() + 2); // 删除索引2位置的元素

    std::list<int> lst = {1, 2, 3};
    lst.push_back(4); // 在末尾添加4
    lst.pop_front(); // 删除头部元素

    return 0;
}

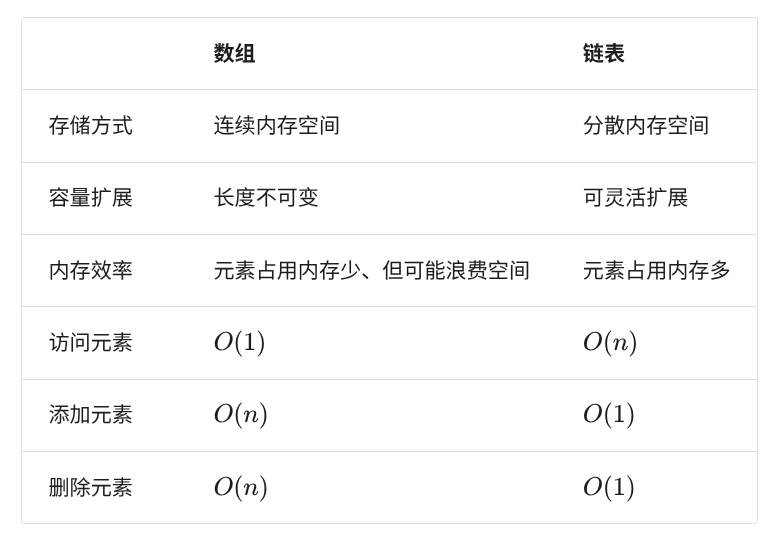
数组（如 vector）支持随机访问（O(1)），尾部增删效率高（均摊 O(1)），但中间位置增删需要移动元素（O(n)）；

链表（如 list）不支持随机访问（O(n)），但在已知节点指针的前提下，任意位置增删效率为 O(1)。

栈和队列是两种线性逻辑结构：栈遵循 “后进先出（LIFO）”，队列遵循 “先进先出（FIFO）”。

它们作为逻辑结构，既可以基于链表实现（链式栈 / 链式队列），也可以基于数组实现（顺序栈 / 循环队列）。

栈（Stack）是遵循后进先出（LIFO）的线性逻辑结构，当我们用链表作为底层存储实现栈时，相当于对链表的操作做限制——只保留在链表一端的插入/删除功能；

队列（Queue）是遵循先进先出（FIFO）的线性逻辑结构，当我们用链表作为底层存储实现队列时，相当于对链表的操作做限制——只保留在链表两端的插入/删除功能。

二、栈的实现

栈（Stack）的实现可以看作一种有限制的链表，链表可以在任意位置进行插入和删除，而栈只能在一端进行插入和删除操作，这一端被称为栈顶（Top）。

经常用来形容栈的结构是“盘子”，我们只能在盘子的一端进行操作，最后放上去的盘子最先被拿走。

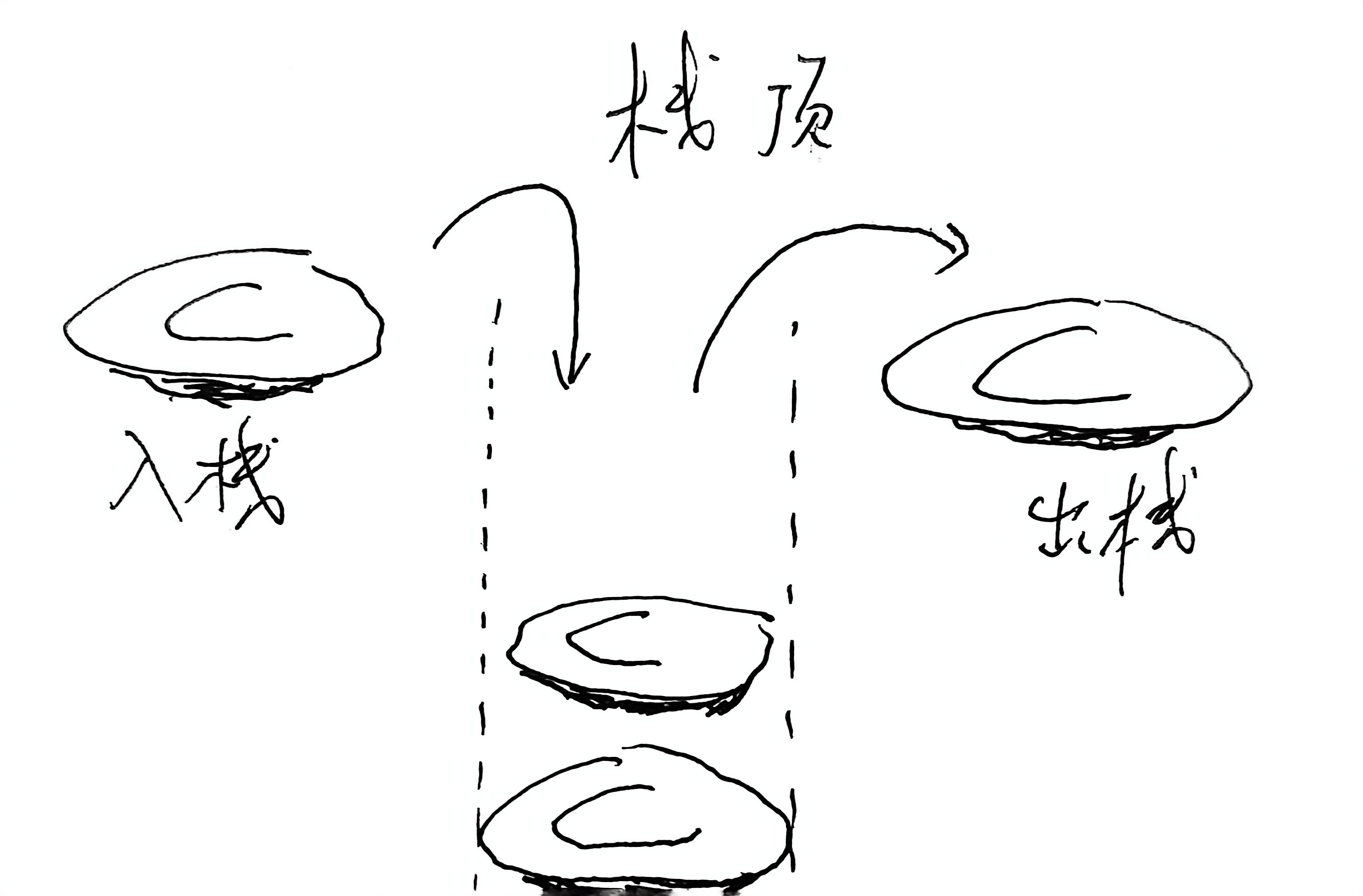
栈遵循后进先出（LIFO）的原则。

也就是说我们可以屏蔽掉链表的其他功能，只保留在链表一端进行插入和删除的功能，这样就实现了栈。

1、基于自定义类实现栈

关键点：

入栈：在链表头部（栈顶）添加元素，时间复杂度 O(1)
出栈：在链表头部（栈顶）删除元素，时间复杂度 O(1)

#include <iostream>
#include <stdexcept>
using namespace std;

// 1. 定义链表节点结构体
template<typename T>
struct ListNode {
    T data_; // 存储数据
    ListNode *next_; // 指向下一个节点的指针

    ListNode(T x) : data_(x), next_(nullptr) {
    }
};

// 2. 基于自定义链表实现栈
template<typename T>
class MyCustomLinkedListStack {
private:
    ListNode<T> *topNode_; // 指向栈顶节点的指针
    int stackSize_; // 记录栈的大小

public:
    MyCustomLinkedListStack() : topNode_(nullptr), stackSize_(0) {
    }

    ~MyCustomLinkedListStack() {
        while (topNode_ != nullptr) {
            ListNode<T> *temp = topNode_;
            topNode_ = topNode_->next_;
            delete temp;
        }
    }

    // 入栈：在链表头部（栈顶）添加元素，时间复杂度 O(1)

    /*
    1、假设当前栈从栈顶到栈底的元素依次为 3 -> 2 -> 1，topNode_ 指向 3。
    2、当我们执行 push(4) 操作时，首先创建一个新节点 newNode，数据为 4。
    3、newNode->next_ = topNode_; 此时链表结构变为 4 -> 3 -> 2 -> 1，newNode 的 next 指向原来的栈顶节点 3。
    4、更新 topNode_ 指针指向 newNode（即 topNode_ = newNode;），此时栈顶元素变为 4。
    5、栈的大小 stackSize_ 增加 1。
    6、最终结果是栈顶元素为 4，栈的结构为 4 -> 3 -> 2 -> 1，栈的大小为原来加 1。
    */

    void push(T x) {
        ListNode<T> *newNode = new ListNode<T>(x);
        newNode->next_ = topNode_; // 新节点的 next 指向当前的栈顶节点
        topNode_ = newNode; // 更新栈顶指针指向新节点
        stackSize_++;
    }

    // 出栈：在链表头部（栈顶）删除元素，时间复杂度 O(1)

    /*
    1、假设当前栈从栈顶到栈底的元素依次为 4 -> 3 -> 2 -> 1，topNode_ 指向 4。
    2、当我们执行 pop() 操作时，首先检查栈是否为空，如果为空则抛出异常。
    3、保存当前栈顶节点的指针 temp = topNode_，以及栈顶元素的值 topVal = temp->data_ 也就是 4。
    4、更新 topNode_ 指针指向下一个节点（即 topNode_ = topNode_->next_;），此时栈顶元素变为 3。
    5、删除原来的栈顶节点 temp，释放内存。
    6、栈的大小 stackSize_ 减少 1。
    7、最终结果是返回被弹出的元素值 4，栈顶元素变为 3，栈的结构为 3 -> 2 -> 1，栈的大小为原来减 1。
    */

    T pop() {
        if (empty()) {
            throw runtime_error("Error: 栈为空，无法执行 pop 操作！");
        }
        ListNode<T> *temp = topNode_;
        T topVal = temp->data_;
        topNode_ = topNode_->next_;
        delete temp;
        stackSize_--;
        return topVal;
    }

    // 查看栈顶元素
    T peek() const {
        if (empty()) {
            throw runtime_error("Error: 栈为空，无法执行 peek 操作！");
        }
        return topNode_->data_;
    }

    // 判断栈是否为空
    bool empty() const {
        return topNode_ == nullptr;
    }

    // 获取栈的大小
    int size() const {
        return stackSize_;
    }
};

// 测试代码
int main() {
    MyCustomLinkedListStack<int> stack;

    // 入栈操作
    stack.push(1);
    stack.push(2);
    stack.push(3);

    // 查看栈顶和大小
    cout << "栈顶元素: " << stack.peek() << endl; // 输出 3
    cout << "栈大小: " << stack.size() << endl; // 输出 3

    // 出栈操作
    cout << "弹出元素: " << stack.pop() << endl; // 输出 3
    cout << "栈顶元素: " << stack.peek() << endl; // 输出 2
    cout << "栈大小: " << stack.size() << endl; // 输出 2

    // 继续出栈
    stack.pop(); // 弹出 2
    stack.pop(); // 弹出 1

    cout << "栈现在" << (stack.empty() ? "为" : "不为") << "空" << endl;

    return 0;
}

栈的入栈相当于在链表头部添加元素，出栈相当于在链表头部删除元素。所以时间复杂度都是 O(1)。

2、基于 list 实现栈

我们可以直接使用 std::list 来实现栈：

方案1：用 push_back/pop_back 实现，此时 list 的尾部对应栈的栈顶；
方案2：用 push_front/pop_front 实现，此时 list 的头部对应栈的栈顶；

两种方案效果一致（都满足栈的LIFO特性），因为栈只要求在“一端”操作，具体对应list的头部/尾部仅为物理实现差异。

#include <iostream>
#include <list>
#include <stdexcept>

template<typename T>
class MyLinkedListStack {
private:
    std::list<T> stack_;
public:
    void push(T x) {
        stack_.push_back(x);
    }

    T pop() {
        if (empty()) {
            throw std::runtime_error("Error: 栈为空，无法执行 pop 操作！");
        }
        T topElement = stack_.back();
        stack_.pop_back();
        return topElement;
    }

    T peek() const {
        if (empty()) {
            throw std::runtime_error("Error: 栈为空，无法执行 peek 操作！");
        }
        return stack_.back();
    }

    bool empty() const {
        return stack_.empty();
    }

    int size() const {
        return stack_.size();
    }
};

int main() {
    MyLinkedListStack<int> stack;
    stack.push(1);
    stack.push(2);
    stack.push(3);
    std::cout << "栈顶元素: " << stack.peek() << std::endl; // 输出 3
    std::cout << "弹出元素: " << stack.pop() << std::endl; // 输出 3
    std::cout << "栈顶元素: " << stack.peek() << std::endl; // 输出 2
    std::cout << "栈大小: " << stack.size() << std::endl; // 输出 2

    // 测试空栈操作
    stack.pop(); // 弹出 2
    stack.pop(); // 弹出 1
    std::cout << "栈是否为空: " << (stack.empty() ? "是" : "否") << std::endl; // 输出 是

    return 0;
}

3、时间复杂度分析

操作	描述	时间复杂度
push()	元素入栈（添加至栈顶）	O(1)
pop()	元素出栈（删除栈顶元素）	O(1)
peek()	查看栈顶元素	O(1)

三、队列的实现

队列（Queue）的实现也可以看作一种有限制的链表，链表可以在任意位置进行插入和删除，而队列只能在两端进行操作：一端进行插入操作，称为队尾（Rear）；另一端进行删除操作，称为队头（Front）。

经常用来形容队列的结构是“排队”，我们只能在队尾进行入队操作，在队头进行出队操作，最先进入队列的元素最先被处理。

队列遵循先进先出（FIFO）的原则。

也就是说我们可以屏蔽掉链表的其他功能，只保留在链表两端进行插入和删除的功能，这样就实现了队列。

1、基于自定义类实现队列

关键点：

入队：在链表尾部（队尾）添加元素，时间复杂度 O(1)
出队：在链表头部（队头）删除元素，时间复杂度 O(1)

#include <iostream>
#include <stdexcept>
using namespace std;

// 1. 定义链表节点结构体
template<typename T>
struct ListNode {
    T data_;
    ListNode *next_;

    ListNode(T x) : data_(x), next_(nullptr) {
    }
};

// 2. 基于自定义链表实现队列
template<typename T>
class MyCustomLinkedListQueue {
private:
    ListNode<T> *frontNode_;
    ListNode<T> *rearNode_;
    int queueSize_;

public:
    MyCustomLinkedListQueue() : frontNode_(nullptr), rearNode_(nullptr), queueSize_(0) {
    }

    ~MyCustomLinkedListQueue() {
        while (frontNode_ != nullptr) {
            ListNode<T> *temp = frontNode_;
            frontNode_ = frontNode_->next_;
            delete temp;
        }
    }

    // 入队：在链表尾部（队尾）添加元素

    /*
    1、假设当前队列从队头到队尾的元素依次为 1 -> 2 -> 3，frontNode_ 指向 1，rearNode_ 指向 3。
    2、当我们执行 enqueue(4) 操作时，首先创建一个新节点 newNode，数据为 4。
    3、如果 rearNode_ 为 nullptr，说明队列为空，此时 frontNode_ 和 rearNode_ 都指向 newNode，队列结构变为 4。
    4、如果 rearNode_ 不为 nullptr，说明队列不为空，此时将 rearNode_->next_ 指向 newNode。
    5、更新 rearNode_ 指针指向 newNode，此时队尾元素变为 4。
    6、队列的大小 queueSize_ 增加 1。
    7、最终结果是队尾元素为 4，队列的结构为 1 -> 2 -> 3 -> 4，队列的大小为原来加 1。
    */

    void enqueue(T x) {
        ListNode<T> *newNode = new ListNode<T>(x);
        if (rearNode_ == nullptr) {
            frontNode_ = rearNode_ = newNode;
        } else {
            rearNode_->next_ = newNode;
            rearNode_ = newNode;
        }
        queueSize_++;
    }

    // 出队：在链表头部（队头）删除元素

    /*
    1、假设当前队列从队头到队尾的元素依次为 1 -> 2 -> 3，frontNode_ 指向 1，rearNode_ 指向 3。
    2、当我们执行 dequeue() 操作时，首先检查队列是否为空，如果为空则抛出异常。
    3、保存当前队头节点的指针 temp = frontNode_，以及队头元素的值 frontVal = temp->data_ 也就是 1。
    4、更新 frontNode_ 指针指向下一个节点（即 frontNode_ = frontNode_->next_;），此时队头元素变为 2。
    5、如果更新后的 frontNode_ 为 nullptr，说明队列已经变空，此时将 rearNode_ 也设置为 nullptr。
    6、删除原来的队头节点 temp，释放内存。
    7、队列的大小 queueSize_ 减少 1。
    8、最终结果是返回被出队的元素值 1，队头元素变为 2，队列的结构为 2 -> 3，队列的大小为原来减 1。
    */

    T dequeue() {
        if (empty()) {
            throw runtime_error("Error: 队列为空，无法执行 dequeue 操作！");
        }
        ListNode<T> *temp = frontNode_;
        T frontVal = temp->data_;
        frontNode_ = frontNode_->next_;
        if (frontNode_ == nullptr) {
            rearNode_ = nullptr;
        }
        delete temp;
        queueSize_--;
        return frontVal;
    }

    // 查看队头元素
    T peek() const {
        if (empty()) {
            throw runtime_error("Error: 队列为空，无法执行 peek 操作！");
        }
        return frontNode_->data_;
    }

    // 判断队列是否为空
    bool empty() const {
        return frontNode_ == nullptr;
    }

    // 获取队列的大小
    int size() const {
        return queueSize_;
    }
};

// 测试代码
int main() {
    MyCustomLinkedListQueue<int> queue;
    // 入队操作
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    // 查看队头和大小
    cout << "队头元素: " << queue.peek() << endl; // 输出 1
    cout << "队列大小: " << queue.size() << endl; // 输出 3
    // 出队操作
    cout << "出队元素: " << queue.dequeue() << endl; // 输出 1
    cout << "队头元素: " << queue.peek() << endl; // 输出 2
    cout << "队列大小: " << queue.size() << endl; // 输出 2
    // 继续出队
    queue.dequeue(); // 出队 2
    queue.dequeue(); // 出队 3
    cout << "队列现在" << (queue.empty() ? "为空" : "不为空") << endl;
    return 0;
}

队列的入队相当于在链表尾部添加元素，出队相当于在链表头部删除元素。所以时间复杂度都是 O(1)。

2、基于 list 实现队列

#include <iostream>
#include <list>
#include <stdexcept>

template<typename T>
class MyLinkedListQueue {
private:
    std::list<T> queue_;
public:
    void enqueue(T x) {
        queue_.push_back(x);
    }

    T dequeue() {
        if (empty()) {
            throw std::runtime_error("Error: 队列为空，无法执行 dequeue 操作！");
        }
        T frontElement = queue_.front();
        queue_.pop_front();
        return frontElement;
    }

    T peek() const {
        if (empty()) {
            throw std::runtime_error("Error: 队列为空，无法执行 peek 操作！");
        }
        return queue_.front();
    }

    bool empty() const {
        return queue_.empty();
    }

    int size() const {
        return queue_.size();
    }
};

int main() {
    MyLinkedListQueue<int> queue;
    queue.enqueue(1);
    queue.enqueue(2);
    queue.enqueue(3);
    std::cout << "队头元素: " << queue.peek() << std::endl; // 输出 1
    std::cout << "出队元素: " << queue.dequeue() << std::endl; // 输出 1
    std::cout << "队头元素: " << queue.peek() << std::endl; // 输出 2
    std::cout << "队列大小: " << queue.size() << std::endl; // 输出 2

    // 测试空队列操作
    queue.dequeue(); // 出队 2
    queue.dequeue(); // 出队 3
    std::cout << "队列是否为空: " << (queue.empty() ? "是" : "否") << std::endl; // 输出 是

    return 0;
}

3、时间复杂度分析

操作	描述	时间复杂度
enqueue()	元素入队（添加至队尾）	O(1)
dequeue()	元素出队（删除队头元素）	O(1)
peek()	查看队头元素	O(1)

四、STL 中的 stack 和 queue

C++ STL 中提供了 stack 和 queue 两个容器适配器，分别用于实现栈和队列的数据结构。

STL 的 stack 和 queue 是容器适配器，默认底层容器为 deque（双端队列），也可指定为 list/vector 等其他容器。

1、STL 中的 stack

#include <iostream>
#include <stack>

int main() {
    std::stack<int> s;

    // 向栈中添加元素
    s.push(10);
    s.push(20);
    s.push(30);

    // 打印栈顶元素
    std::cout << "Top element is: " << s.top() << std::endl; // 输出: Top element is: 30

    // 移除栈顶元素
    s.pop();
    std::cout << "After popping, top element is: " << s.top() << std::endl; // 输出: After popping, top element is: 20

    // 检查栈是否为空
    if (!s.empty()) {
        std::cout << "Stack is not empty." << std::endl; // 输出: Stack is not empty.
    }

    // 打印栈的大小
    std::cout << "Size of stack: " << s.size() << std::endl; // 输出: Size of stack: 2

    // 继续移除元素
    s.pop();
    s.pop();

    // 检查栈是否为空
    if (s.empty()) {
        std::cout << "Stack is empty." << std::endl; // 输出: Stack is empty.
    }

    return 0;
}

2、STL 中的 queue

#include <iostream>
#include <queue>

int main() {
    // 创建一个整数队列
    std::queue<int> q;

    // 向队列中添加元素
    q.push(10);
    q.push(20);
    q.push(30);

    // 打印队列中的元素数量
    std::cout << "队列中的元素数量: " << q.size() << std::endl;

    // 打印队首元素
    std::cout << "队首元素: " << q.front() << std::endl;

    // 打印队尾元素
    std::cout << "队尾元素: " << q.back() << std::endl;

    // 移除队首元素
    q.pop();
    std::cout << "移除队首元素后，队首元素: " << q.front() << std::endl;

    // 再次打印队列中的元素数量
    std::cout << "队列中的元素数量: " << q.size() << std::endl;

    return 0;
}