一、原文
在全国高考中,本节主要考查集合的概念、关系、运算等,下面梳理一些常考知识点
1、集合中元素的性质
确定性,互异性,无序性
2、集合间的基本关系
| 关系 | 自然语言 | 符号语言 |
|---|
| 子集 | 集合 A 中的元素都在集合 B 中 | A⊆B |
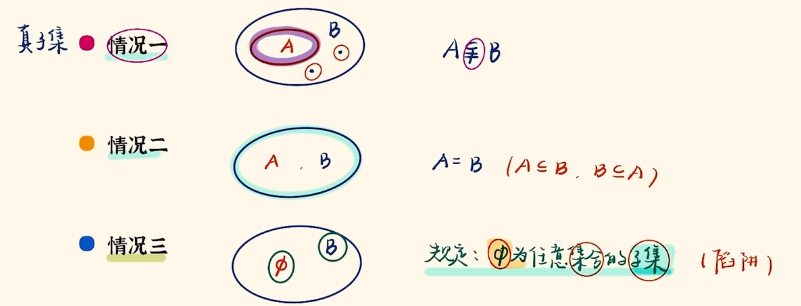
| 真子集 | 集合 A 是集合 B 的子集,且集合 B 中至少有一个元素不在集合 A 中 | A⫋B |
| 集合相等 | 集合 A、B 中的元素相同或集合 A、B 互为子集 | A=B |
3、子集个数
当 n 个元素的集合的子集有 2n 个,非空子集有 2n−1 个,真子集有 2n−1 个,非真空子集有 2n−2(n≥1) 个
4、集合的基本运算
| 运算 | 自然语言 | 符号语言 |
|---|
| 并集 | 由所有属于集合 A 或属于集合 B 的元素组成的集合 | A∪B={x∣x∈A 或 x∈B} |
| 交集 | 由属于集合 A 且属于集合 B 的所有元素组成的集合 | A∩B={x∣x∈A 且 x∈B} |
| 补集 | 由全体 U 中不属于集合 A 的所有元素组成的集合 | ∁UA={x∣x∈U 且 x∈/A} |
二、原文深度解析
1、概念
集合(set)简称集,是一个基本的 [数学模型],指 [若干] [不同] [对象] 形成的总体
| 名称 | 解释 | 举例 |
|---|
| 数学模型 | 是使用数学来将一个系统简化后予以描述 | 概率模型 |
| 若干 | 表示不定量 | 零、一、多、无限 |
| 不同 | 互不相同 | {21,0.5} 不是集合 |
| 对象 | 任何被演绎推理和数学证明正式定义的对象 | 数、集合、函数、表达式、几何形状 |
其他细节:
- 集合里的对象称作元素或成员,它们可以是任何类型的数学对象:数字、符号、变量、空间中的点、线、面,甚至是其他集合
- 若 x 是集合 A 的元素,记作 x∈A
- 不包含任何元素的集合称为空集;只包含一个元素的集合称为单元素集合
- 集合可以包含有限或无限个元素
- 如果两个集合所包含的元素完全相同,我们称这两个集合相等
2、性质
集合 [元素的性质] 有 [确定性]、[互异性]、[无序性]
| 名称 | 解释 | 举例 |
|---|
| 元素的性质 | 元素之间的性质,不是指集合之间 | 集合没有互异性,两个集合可以相等 |
| 确定性 | 给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现 | 比王俊凯帅的男孩不构成集合 |
| 互异性 | 一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次 | |
| 无序性 | 一个集合中,每个元素的地位都是相同的,元素之间是无序的 | |
互异性常考类型:集合相等
已知 {a,ab,1}={a2,a+b,0},则 a2022+b2023=________
思考方式 1:从待定元素 → 已知值
-
当 a=a2 时,a=−1
- 当 ab=a+b 时,b=21,此时 {−1,−21,1}={1,−21,0},不符合题意。
- 当 ab=0 时,b=0,此时 {−1,0,1}={1,−1,0},符合题意。
-
当 a=a+b 时,b=0,此时 {a,0,1}={a2,a,0}
所以 a2=1 则 a=−1,此时 {−1,0,1}={1,−1,0},符合题意。
-
当 a=0 时,不符合题意
综上,a=−1,b=0
思考方式 2:从已知值 → 待定元素
-
从 1 出发
- 当 1=a2 时,a=−1,同上,a=−1,b=0
- 当 1=a+b 时,此时只能是 b=0,a=1,不符合题意。
-
从 0 出发
只能是 b=0,此时 {a,0,1}={a2,a,0},同上 a=−1
综上,a=−1,b=0
对比总结:
3、集合之间的关系
-
空集 ∅
-
空集是什么:
- 年龄大于 200 岁的活人
- 大于 3 小于 2 的实数
- 绝对值等于 −1 的实数
以上能构成集合,满足集合的性质,但不包含任何元素
-
空集的简单考法
已知集合 M={x∣2m<x<m+1},且 M∈∅,则实数 m 的取值范围是:________
因为 M 是空集,所以 M 中不包含任何元素,即区间下限大于等于区间上限。
2m>m+1 还是 2m≥m+1?
大胆猜想,小心求证:先试一下 2m=m+1→m=1,恰好 m=1 符合题意
问取值范围时要用集合来答,即取值范围是 {m∣m≥1}
三、子集个数公式证明
证明:若集合 A 含有 n 个元素,则 A 的子集总个数为 f(n)=2n
参考视频如下
证法 1(分类法和递推公式)
第一步:当集合 A=∅ 时,其子集只有空集,f(0)=20=1,显然公式成立
第二步:当集合 A=∅ 时,设集合 A={a1,a2,…,an} 含有 n 个元素
则集合 A 的子集可分为两类
| 分类 | 描述 | 数学语言 |
|---|
| 类 1 | 不含有 a1 的子集 | {a2,a3,…,an} 的所有子集 |
| 类 2 | 含有 a1 的子集 | |
举个例子:若 A={1,2,3,4}
则:A 的子集有:{1234}、{123}、{124}、{134}、{234}、{12}、{13}、{14}、{23}、{24}、{34}、{1}、{2}、{3}、{4}、∅
第一类有:{234}、{23}、{24}、{34}、{2}、{3}、{4}、∅
第二类有:{1234}、{123}、{124}、{134}、{12}、{13}、{14}、{1}
第一类共有 n−1 个元素,所以共有 f(n−1) 种子集
第二类可看作第一类每个子集都添加一个元素 a1而成,所以第二类子集个数为 f(n−1)
又由于总子集个数 = 第一类 + 第二类,即
f(n)=f(n−1)+f(n−1)=2f(n−1)
重复应用上述递推公式可得
f(n)=2f(n−1)=22f(n−2)=23f(n−3)=⋯=2nf(0)=2n⋅1=2n
证毕!
证法 2(乘法计数原理)
对于集合 A 中任意子集 B,那么集合 A 中元素 ai 要么 ai∈B 要么 ai∈/B
根据分步乘法计数原理,从 a1 到 ai 考虑 n 步,每一步都有 2 种可能的情况,故 A 的子集有 2n 个
证法 3(数学归纳法)
第一步:当 n=0,1 时,f(0)=1,f(1)=2 显然公式成立
第二步:假设当 n=k 时公式成立,f(k)=2k
则当 n=k+1 时,可设 A={a1,a2,…,ak,ak+1}
此时 A 的子集可分为两类
| 分类 | 描述 | 子集个数 |
|---|
| 类 1 | 不含有 ak+1 的子集 | {a1,a2,…,ak} 的子集 =f(k) |
| 类 2 | 含有 ak+1 的子集 | f(k) |
则 f(k+1)=2f(k)=2k+1
所以当 n=k+1 时,公式成立
最后根据数学归纳法原理可证得公式对于一切非负整数 n 都成立
故证毕!
证法 4(组合数和二项式定理)
二项式定理:(a+b)n=Cn0anb0+Cn1an−1b1+…+Cnna0bn=∑k=0nCnkan−kbk
当 a=b=1 时,等式变为:(1+1)n=2n=Cn0+Cn1+…+Cnn
组合数:从 n 个不同元素中,不管顺序抽出 m 个不同元素,其中组合种数称为组合数:Cnm=m!(n−m)!n!
首先,设集合 A 的元素个数为 n,其子集的组成元素个数为 k。
- 当 k=0 时:∅⟶Cn0
- 当 k=1 时:{a1},{a2},…,{an}⟶Cn1
- 当 k=2 时:{a1,a2},{a1,a3},{a1,a4},…⟶Cn2
- …
- 当 k=n 时:{a1,a2,a3,…,an}⟶Cnn
集合 A 的子集总个数为:Cn0+Cn1+…+Cnn=∑k=0nCnk=2n
证毕!
四、补充
1、常见数集
| 数集 | 符号 | 举例 |
|---|
| 自然数集 | N | 0,1,2,3,… |
| 正整数集 | N+ | 1,2,3,… |
| 整数集 | Z | 0,1,−1,2,−2,… |
| 有理数集 | Q | |
| 实数集 | R | 有理数、无理数 |
| 复数集 | C | a+bi |
2、集合的表示方法
-
列举法
| 举例 | 表示 |
|---|
| 大于 1 小于 5 的整数构成的集合 | A={2,3,4} |
| 绝对值小于 3 的整数构成的集合 | A={0,−1,−2,,1,2} |
| 所有偶数构成的集合 | A={2,4,6,8,…} |
| 第一象限所有的点构成的集合 | 无法列举 |
-
描述法
| 举例 | 表示 |
|---|
| 大于 1 小于 5 的整数构成的集合 | A={x∣1<x<5,x∈Z} 或 A={x∈Z∣1<x<5} |
| 绝对值小于 3 的整数构成的集合 | A={x∣∣x∣<3,x∈Z} |
| 所有偶数构成的集合 | A={x∣x=2k,k∈Z} |
| 第一象限所有的点构成的集合 | A={x∣x=(x,y),x>0,y>0,x∈R,y∈R} |