取整函数
R 提供了几个用于对小数进行取整的函数,这些函数包括 round 、 ceiling 、 floor 、 trunc 和 signif 函数
round 函数
R 中最常见的取整函数就是 round 函数。它会把小数进行四舍五入为最接近的整数,如果小数部分等于 0.5,则取离它最近的偶数。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
round(x)
# 输出 2 4 6 9 -2 -8 -11
这种取整方法称作半偶数舍入(Round Half to Even),也称为“银行家舍入”或“四舍、六入、五留双”
比如十进制:
0.5 --> 0
1.5 --> 2
2.5 --> 2
3.5 --> 4
这种半偶数舍入的方法采用的是一种统计学上更为合理的取整方式,能够减少累积误差
对比四舍五入和半偶数舍入的区别:
| 数据 | 四舍五入 | 半偶数舍入 |
|---|---|---|
| 0 | 0 | 0 |
| 0.5 | 1 | 0 |
| 1 | 1 | 1 |
| 1.5 | 2 | 2 |
| 2 | 2 | 2 |
| 2.5 | 3 | 2 |
| 3 | 3 | 3 |
取总和分别为:10.5、12、10
可看出半偶数舍入将一半向下舍入(前一个数字为偶数),一半向上舍入(前一个数字为奇数)来保持总和更稳定,因此舍入的效果大致抵消
但是此函数主要用例是使用名为 digits 的参数将值取整到特定的小数位数,比如取整小数点后两位:round(x, digits = 2) 或者 round(x, 2)
x <- c(2.153, 4.557, 5.665, 9.1255)
round(x, 2)
# 输出 2.15 4.56 5.66 9.13
可能你会疑问为什么 9.1255 为什么取整后是 9.13 而不是 9.12?这是因为刚才上文提到:它会把小数进行四舍五入为最接近的整数,如果小数部分等于 0.5,则取离它最近的偶数。
所以当我们用 round(9.1255, 2) 时,如果舍入位恰好等于 0.5(即后面全是 0),则才会取离它最近的偶数,即才会触发银行家舍入
而当前的舍入位是 0.0055,大于 0.005,因此会直接四舍五入到 9.13
请注意,如果 digits 参数为负数,则会将数字舍入到小数点左侧的位数
x <- c(2, 4.5, 5, 5.1, 10, 15, -10.5, -10.51)
round(x, digits = -1)
# 输出 0 0 0 10 10 20 -10 -10
当 digits = -1 时,round() 把数值“按 10 位”取整,也就是保留到十位(个位及以下的数字全部变为 0)。
负号只表示方向,不影响舍入规则本身;规则仍然是:
- 先看真正要被舍掉的那一位(个位)上的数字
- 如果是 0–4 → 向下舍
- 如果是 6–9 → 向上入
- 如果恰好是 5 且后面全是 0 → “五留双”(取离它最近的偶数十位)
逐项验证:
| 原值 | 看个位数字 | 规则说明 | 结果 |
|---|---|---|---|
| 2 | 2 | 个位 2 < 5 → 向下舍 | 0 |
| 4.5 | 4 | 个位 4 < 5 → 向下舍 | 0 |
| 5 | 5 | 个位 5 且后面全 0 → 五留双 | 0 |
| 5.1 | 5 | 个位 5 后非 0(.1)→ 六入 | 10 |
| 10 | 0 | 个位 0 < 5 → 向下舍 | 10 |
| 15 | 5 | 个位 5 且后面全 0 → 五留双 | 20 |
| –10.5 | 0 | 个位 0 < 5 → 向下舍 | –10 |
| –10.51 | 0 | 个位 0 < 5 → 向下舍 | –10 |
当 digits = -k 时,把数值按 位取整即可。
同理如下:
round(15,-1) # 20
round(15,-2) # 0
round(55,-2) # 100
floor 和 ceiling 函数
floor 函数用于向下取整,即返回小于或等于给定值的最大整数。它不会进行四舍五入,而是直接向下取整到最接近的整数。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
floor(x)
# 输出 2 4 5 9 -2 -9 -11
floor 的反函数是 ceiling ,它将值向上舍入为不小于该值本身的最小整数。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
ceiling(x)
# 输出 2 5 6 10 -1 -8 -10
这两个函数与 round(x) 的半偶数舍入不同,它们没有“四舍六入五留双”的逻辑,而是无条件地向下或向上取整。
它们的优势主要体现在业务语义简单、可预测、易实现。比如某些运营商不足一分钟按一分钟收费
满足“绝不超发/绝不缺额”这类硬性业务约束,代价是单次和长期都可能出现系统性偏差。
trunc 函数
trunc 函数用于截断小数部分,直接返回整数部分。它不会进行四舍五入,而是简单地去掉小数部分。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
trunc(x)
# 输出 2 4 5 9 -1 -8 -10
trunc(truncate,截断)的核心优势只有一句话:速度最快、规则最简单、结果绝对可预测,且天然满足“只保留整数部分,绝不引入额外偏移”的需求。
signif 函数
signif 函数用于将值舍入到指定的有效数字位数(默认为 6 位)。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
signif(x)
# 输出 2.0000 4.5000 5.6534 9.1800 -1.5000 -8.3500 -10.7800
此函数还允许您使用 digits 参数指定所需的有效数字数。
x <- c(2, 4.5, 5.6534, 9.18, -1.5, -8.35, -10.78)
signif(x, digits = 3)
# 输出 2.00 4.50 5.65 9.18 -1.50 -8.35 -10.80
至于这里你可能会疑惑 signif(2) 为什么显示的是 2.0000 而不是 2.00000。以及 signif(-10.78) 为什么显示的是 -10.80 而不是 -10.8。
这是因为打印规则和计算规则不是一套东西,signif() 计算时的确会保留 6 位有效数字,但打印时会根据实际情况进行格式化。
最值函数
R 中最值函数有 max、min、pmax、pmin。
max 和 min 函数
max 和 min 将分别返回单个向量的最大值和最小值,它只返回一个值。
x <- c(45, 12, 12, 15, 61, 56)
max(x)
min(x)
# 输出:61 12
但是,如果向量包含缺失值( NA ),则该函数将返回 NA 。
x <- c(45, 12, 12, NA, 15, 61, 56)
max(x)
# 输出:NA
如果您想避免这种情况,可以将函数的 na.rm 参数设置为 TRUE ,这样在获取最大值之前就会删除缺失值。
x <- c(45, 12, 12, NA, 15, 61, 56)
max(x, na.rm = TRUE)
# 输出:61
pmax 和 pmin 函数
pmax 和 pmin 函数用于计算多个向量的逐元素最大值和最小值。它们可以接受多个向量作为参数,并返回一个新的向量,其中每个元素是对应位置上所有输入向量的最大值或最小值。
x1 <- c(45, 12, 12, 15, 61, 56)
x2 <- c(15, 35, 81, 23, 45, 24)
x3 <- c(52, 12, 41, 35, 17, 16)
pmax(x1, x2, x3)
# 输出:52 35 81 35 61 56
返回的第一个值是 52,因为它是 45、15 和 52 之间的最大值;返回的第二个值是 35,因为它是 12、35 和 12 之间的最大值,以此类推。
如果向量的长度不一致,pmax 和 pmin 函数会自动将短向量扩展到与最长向量的长度一致。
x1 <- c(45, 12, 12, 15, 30, 56)
x2 <- c(15, 35, 81)
x3 <- c(52, 12)
pmax(x1, x2, x3)
# 输出:52 35 81 15 52 81
扩展的方式是循环补齐
x2 补齐后:15 35 81 15 35 81
x3 补齐后:52 12 52 12 52 12
最后输出的 81 是在 12、81、52 中最大的值;35 是在 15、15、12 中的最大值;52 是在 30、35、52 中的最大值...
这种“循环补齐 + 逐元素比较”的设计,优势可以一句话概括为:用最少的代码,让不同长度、成组比较的向量运算既简洁又符合向量化思维,同时保持与 R 其它运算一致的回收(recycling)语义。
平方根
一个数的平方根是指一个数乘以自身等于该数的数。例如,4 的平方根是 2,因为
sqrt 函数
在 R 中,sqrt 函数用于计算一个数的平方根。例如:
sqrt(4)
# 输出 2
同时,还可以输入数字向量,因此该函数将返回该向量每个元素的平方根。
sqrt(c(1, 4, 9))
# 输出 1 2 3
如果想计算 N 次方根,可以使用 ^ 运算符来手动计算,比如 8 的三次根:
8^(1/3)
# 输出 2
指数和对数
可以利用 R 提供的函数来计算对数和指数: log 函数用于计算自然对数,而 exp 函数用于计算指数。
log 函数
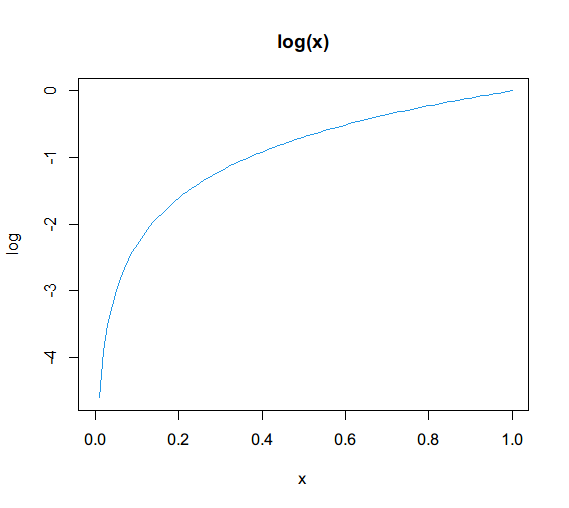
log 函数用于计算自然对数,exp(1) 返回 e 的值(约等于 2.71828),log(x) 默认返回 x 的自然对数。
log(1) # 输出 0
log(exp(1)) # 输出 1
同时可以自定义底数,例如:
log(9, 3) # 输出 9 的 3 的对数
log(8, 2) # 输出 8 的 2 的对数
# 输出 2 3
exp 函数
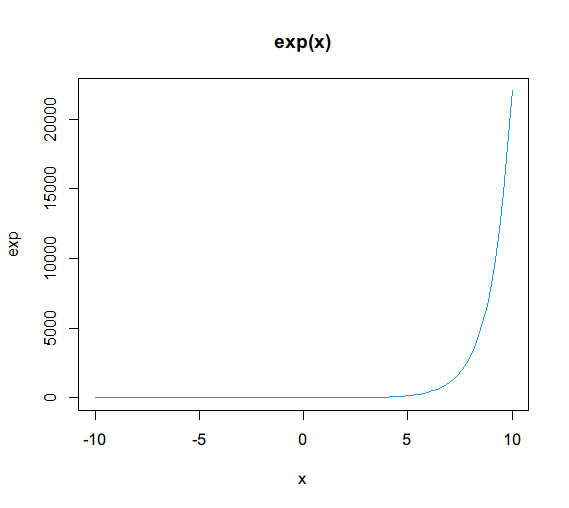
exp 函数用于计算 e 的幂次方,exp(x) 返回 e 的 x 次方。
exp(10)
exp(0)
exp(-5)
exp(4)
# 输出 22026.47 1 0.006737947 54.59815
plot 绘图函数
plot 函数可以用来绘制函数图像,下面是绘制自然对数的 log 和 exp 函数的示例:
plot(log, 0, 1, col = 4, main = "log(x)")
plot(exp, -10, 10, col = 4, main = "exp(x)")
三角函数
R 提供了几个计算三角函数的函数,例如 cos()、sin()、tan()、acos()、asin() 和 atan() 函数,用于计算正弦、余弦、正切、反余弦、反正弦和反正切。
cos、sin 和 tan 函数
cos(pi/3) # 输出 0.5
sin(pi/6) # 输出 0.5
tan(pi/4) # 输出 1
可以使用 plot 函数绘制这些函数的图像:
plot(cos, 0, 2 * pi, col = 4, main = "cos(x)")
plot(sin, 0, 2 * pi, col = 4, main = "sin(x)")
plot(tan, -2 * pi, 2 * pi, col = 4, main = "tan(x)")
反三角函数
acos(0.5) # 输出 1.0472
asin(0.5) # 输出 0.5236
atan(1) # 输出 0.7854
可以使用 plot 函数绘制这些函数的图像:
plot(acos, -1, 1, col = 4, main = "acos(x)")
plot(asin, -1, 1, col = 4, main = "asin(x)")
plot(atan, -10, 10, col = 4, main = "atan(x)")
矩阵运算
R 中可以执行多种矩阵运算,包括:加法、减法、乘法、计算幂、秩、行列式、对角线、特征值和特征向量、转置以及使用不同方法分解矩阵
由于篇幅太长,请期待下一篇文章