
旁氏表
旁氏表(英语:Punnett square),又称棋盘法或者配子法
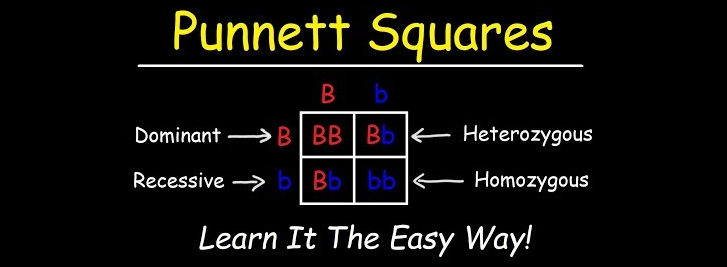
是用于预测特定杂交或育种实验结果的一种图表,是杂交中研究的每个基因的母系等位基因和父系等位基因的每一种可能组合的汇总
概率的加法和乘法
在研究基因杂交之前,最好先了解一下概率的计算
乘法规则
两个或多个独立事件同时发生的概率可以通过将事件各自的概率相乘来计算
比如,抛硬币正面向上的概率是 1/2,并且两次抛硬币是独立事件,所以两次都是正面向上的概率是 1/2 * 1/2 = 1/4
一般来说,你可以将乘法规则视为“与”规则:如果事件 X 和事件 Y 都必须发生才能产生某个结果,并且 X 和 Y 彼此独立(不会影响彼此的可能性),那么你可以使用乘法规则通过将 X 和 Y 的概率相乘来计算结果的概率
加法规则
多个互斥事件的并的概率等于这些事件各自概率之和
比如,抛硬币正面向上的概率是 1/2,反面向上是 1/2,并且不能同时抛出正面和反面都向上,所以抛出 “正面或反面向上” 是由 “正面向上” 和 “反面向上” 组成,概率是 1/2 + 1/2 = 1
再比如,掷一个六面骰子,掷出任意给定数字的概率都是 1/6,但每次只能掷出一个数字,所以掷出 “1 或 6” 是由 “掷出 1” 和 “掷出 6” 组成, 因此掷出 “1 或 6” 的概率为:1/6 + 1/6 = 1/3
| 互斥事件 | 组成 | 概率 |
|---|---|---|
| 硬币抛出正面或反面 | 抛出正面 + 抛出反面 | 1/2 + 1/2 = 1 |
| 六面骰子掷出任意数字 | 掷出 1 + 掷出 2 + 掷出 3 + 掷出 4 + 掷出 5 + 掷出 6 | 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 |
| 六面骰子掷出 1、2 或 3 | 掷出 1 + 掷出 2 + 掷出 3 | 1/6 + 1/6 + 1/6 = 1/2 |
| 扑克牌抽到任意花色的A | 方片 A + 梅花 A + 红心 A + 黑桃 A | 1/52 + 1/52 + 1/52 + 1/52 = 1/13 |
| 扑克牌抽到红心的任意一张 | 红心 A + 红心 2 + 红心 3 + 红心 4 + .... + 红心 Q + 红心 K | 1/52 + 1/52 + 1/52 + 1/52 + 1/52 + 1/52 + ... = 1/4 |
| 五个颜色球的袋子中摸出任意颜色的球 | 颜色 1 + 颜色 2 + 颜色 3 + 颜色 4 + 颜色 5 | 1/5 + 1/5 + 1/5 + 1/5 + 1/5 = 1 |
所以在下文中会出现 “求 Aa 后代为显性” 这是一个互斥事件,有三个事件可以导致显性:
- 两个 A 配子相遇(产生 AA 基因型),或
- 妈妈的 A 配子与爸爸的 a 配子相遇(产生 Aa 基因型),或
- 妈妈的 a 配子与爸爸的 A 配子相遇(产生 Aa 基因型)
使用上面提到的乘法规则,我们可以发现每个单独事件的概率为 1/2 * 1/2 = 1/4,因此后代具有显性表型的概率为:1/4 + 1/4 + 1/4= 3/4
单基因杂交(分离定律)
假如两个生物基因型都是 Aa,则他们分别可以产生 A 和 a 的配子,配子之间的随机结合得到子代的基因型,如下图所示
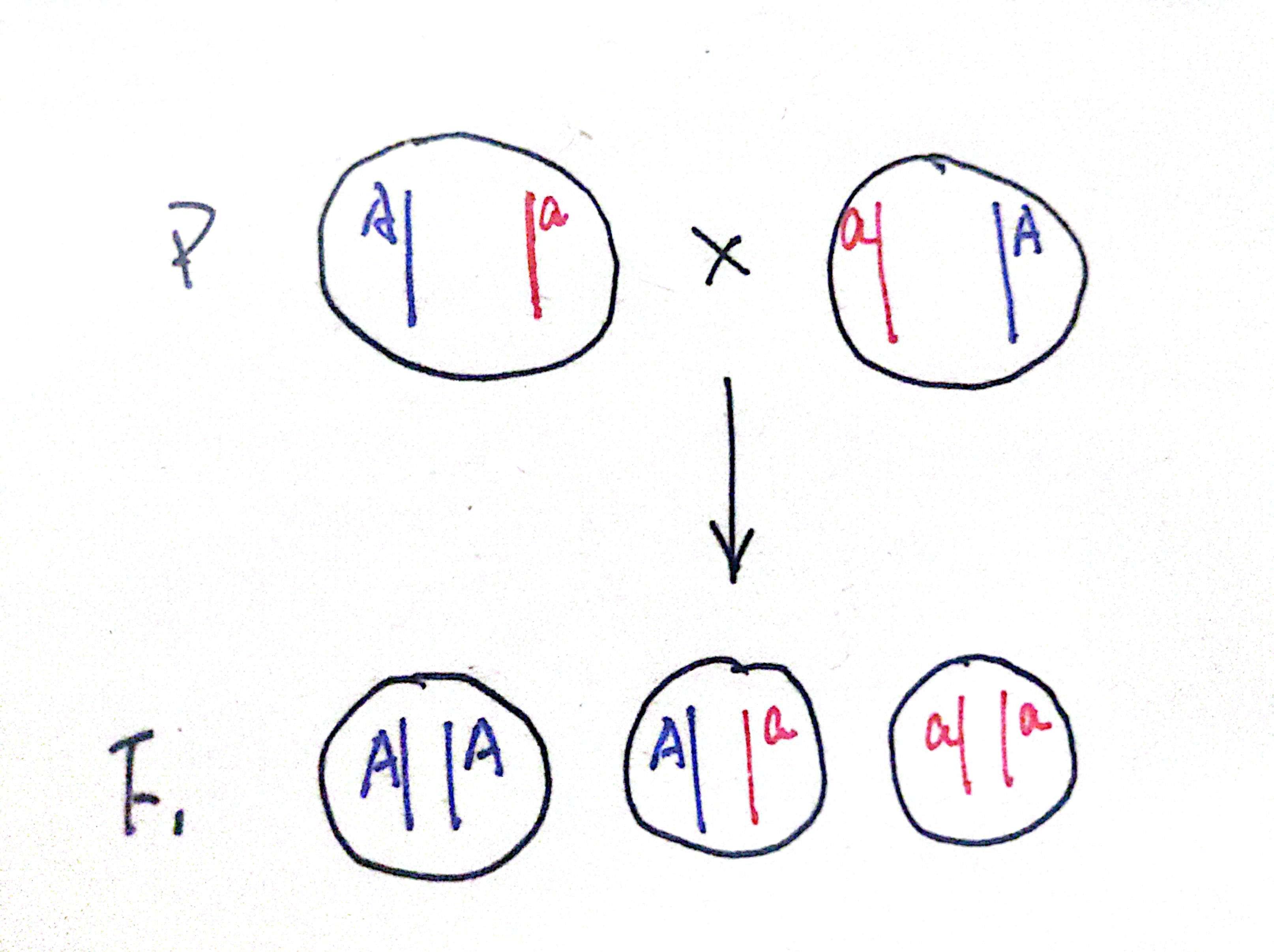
其中 P 表示亲代、F 表示子代
这个过程之间会发生减数分裂,我们将精子或卵子称作配子,我们都知道在减数分裂中染色体复制一次,细胞分裂两次,所以配子的形成经历了如下过程(雌性类似):
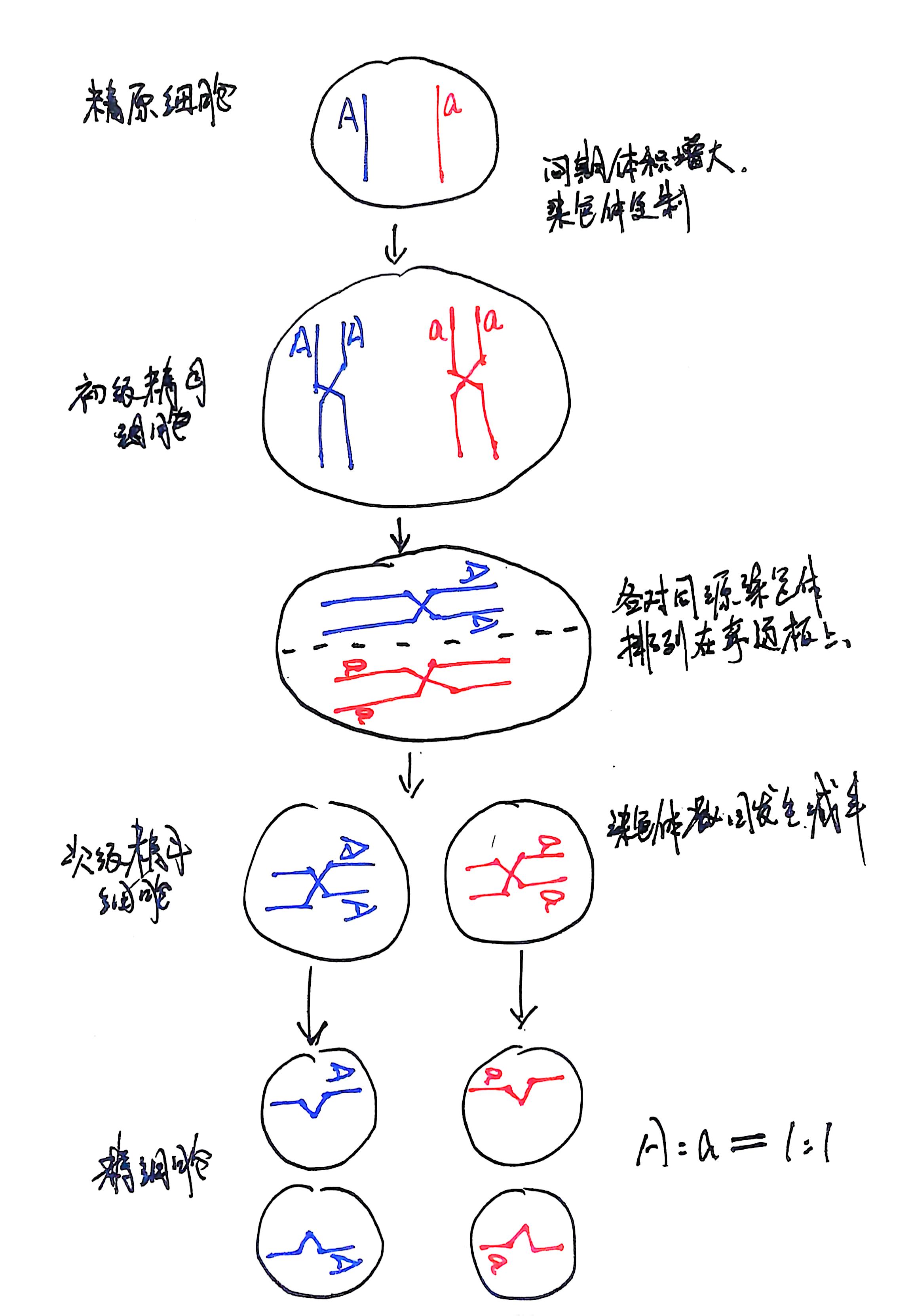
由于只体现一对等位基因,所以没有画联会,也不考虑交叉互换
最后的 A 和 a 各占 50%,所以双方棋盘里的棋子都是 A 和 a
让我们来算算 aa 发生的概率:
母亲提供 a 基因和父亲提供 a 基因这两个事件相互独立不会影响彼此,所以会用到乘法规则
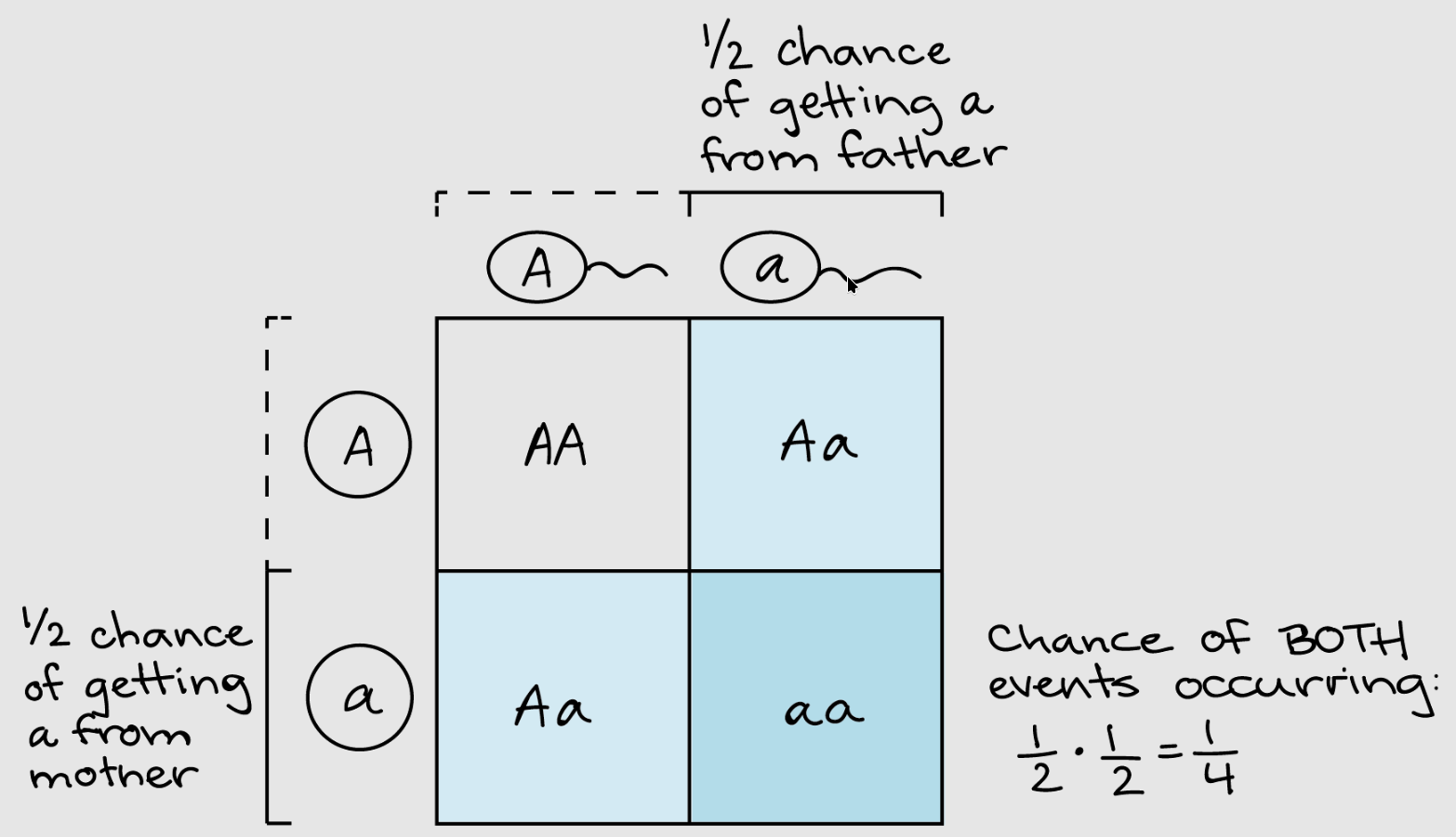
由于父母双方提供 a 的概率都是 1/2,所以 aa 的可能性为:(母亲贡献 a 的概率)x(父亲贡献 a 的概率)= 1/2 * 1/2 = 1/4
并且产生不同基因型是一个构成互不相容的完备事件组,所以基因型的概率和为 1,刚才计算了 aa 即隐性概率是 1/4, 那么显性概率则是 3/4,我们也可以直接相加计算:
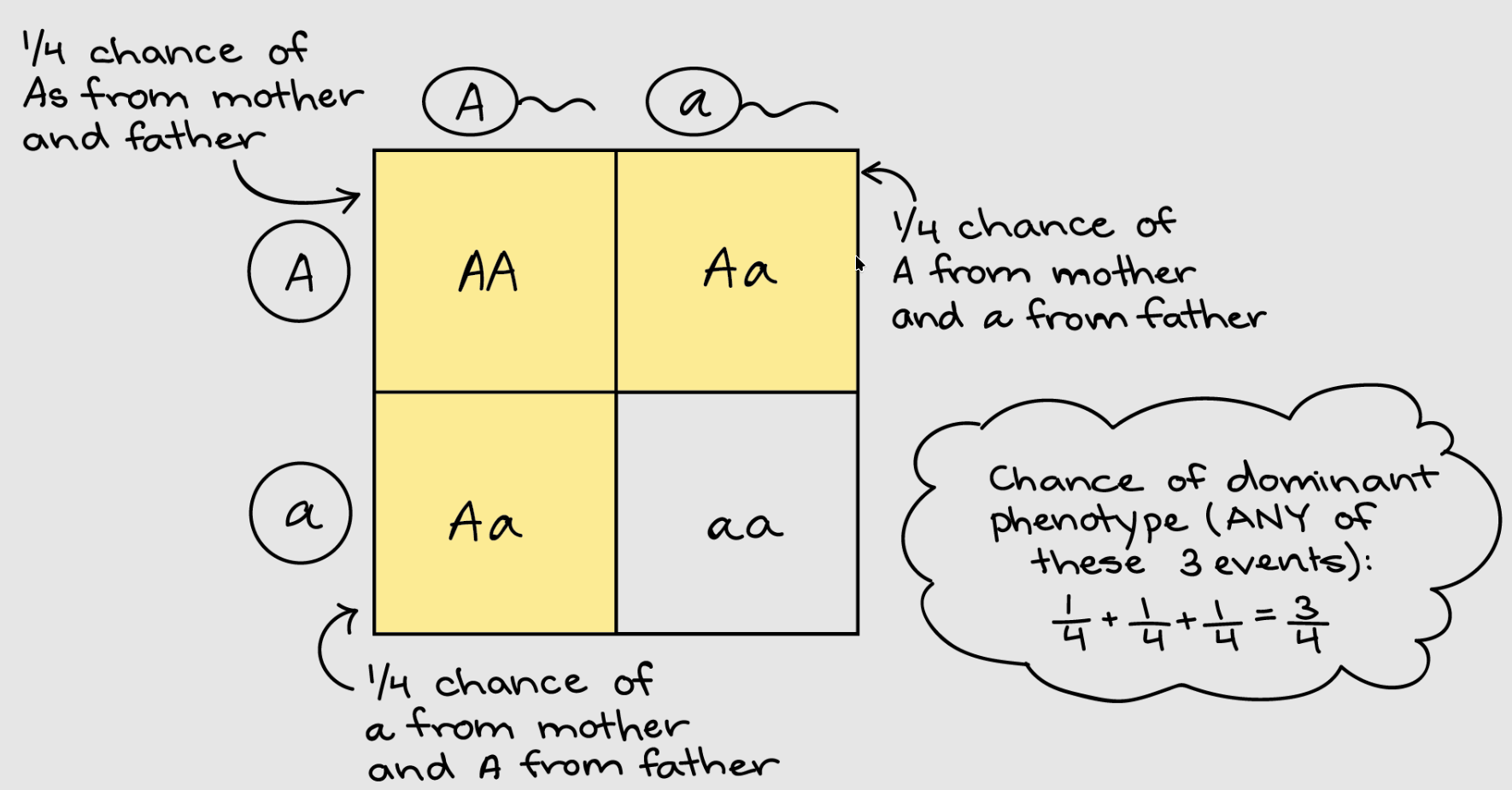
到此,得出 Aa 后代显隐性之比为 3:1(依赖基因的分离定律)
双基因杂交(自由组合定律)
上面的一对等位基因的杂交并不常见,更常见的还是多对等位基因进行杂交,比如有两对等位基因组成的 YyRr 产生配子的过程如下:
首先同源染色体会进行联会配对
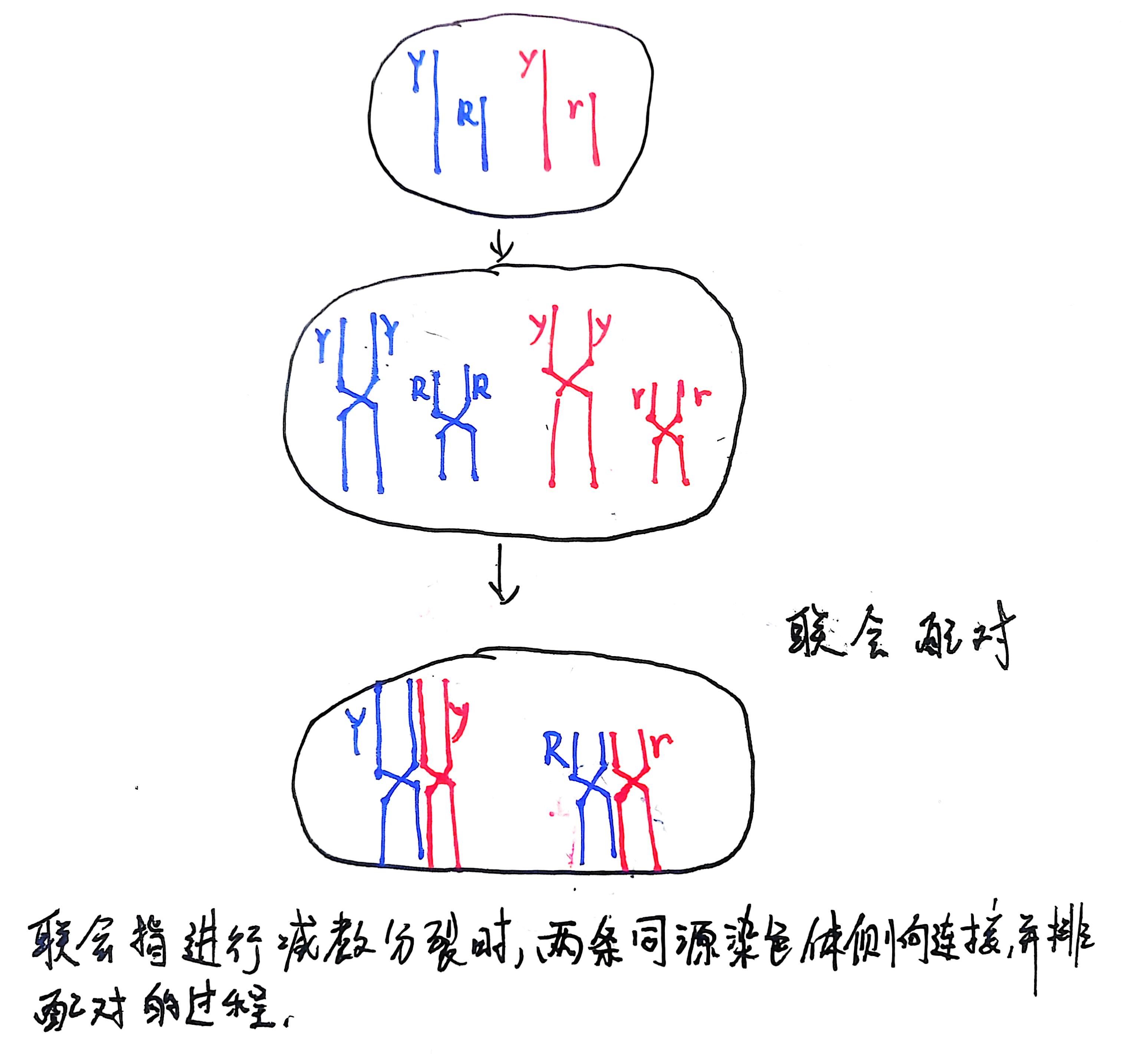
这里的两对等位基因位于不同染色体上独立遗传,并且不考虑互换
这里的联会配对是一个小插曲
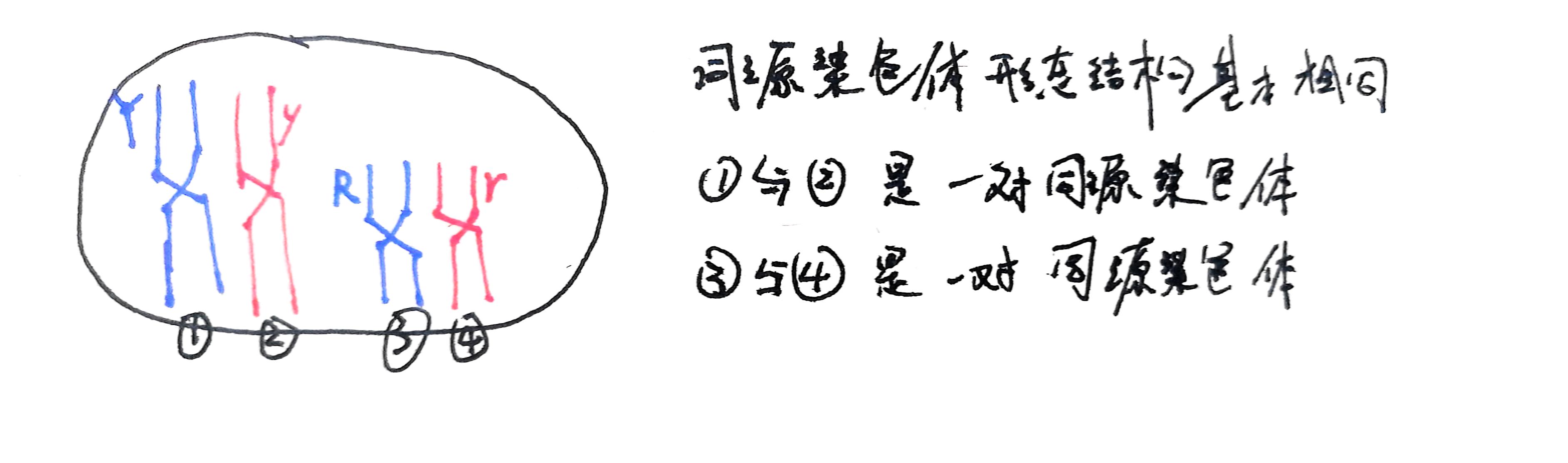
一对同源染色体中有两条染色体、四条姐妹染色单体。联会的目的就是为了见完最后一面再拆散她们,下文会详细解释
联会后,在同源染色体上的等位基因彼此分离的同时,非同源染色体上的非等位基因自由组合,这句话听起来绕口,但是很好理解
先来看看同源染色体上的等位基因彼此分离:
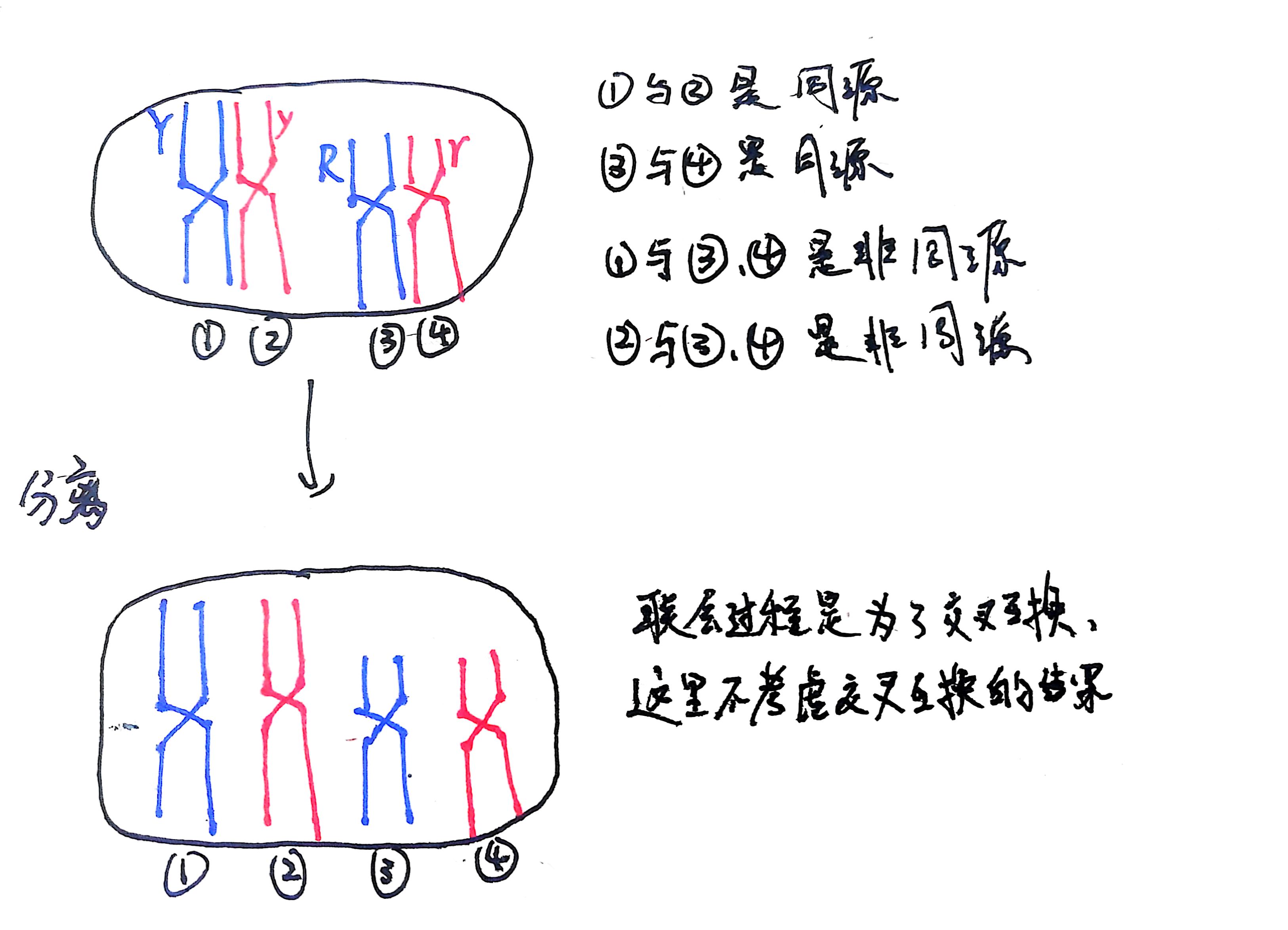
其实分离后与联会前基本一样,那为什么还要联会呢?刚才说了联会就是为了见完最后一面再拆散她们,见面的过程中会互留信物,称作交叉互换,但是这里不考虑交叉互换的情况
再来看看非同源染色体上的非等位基因自由组合:
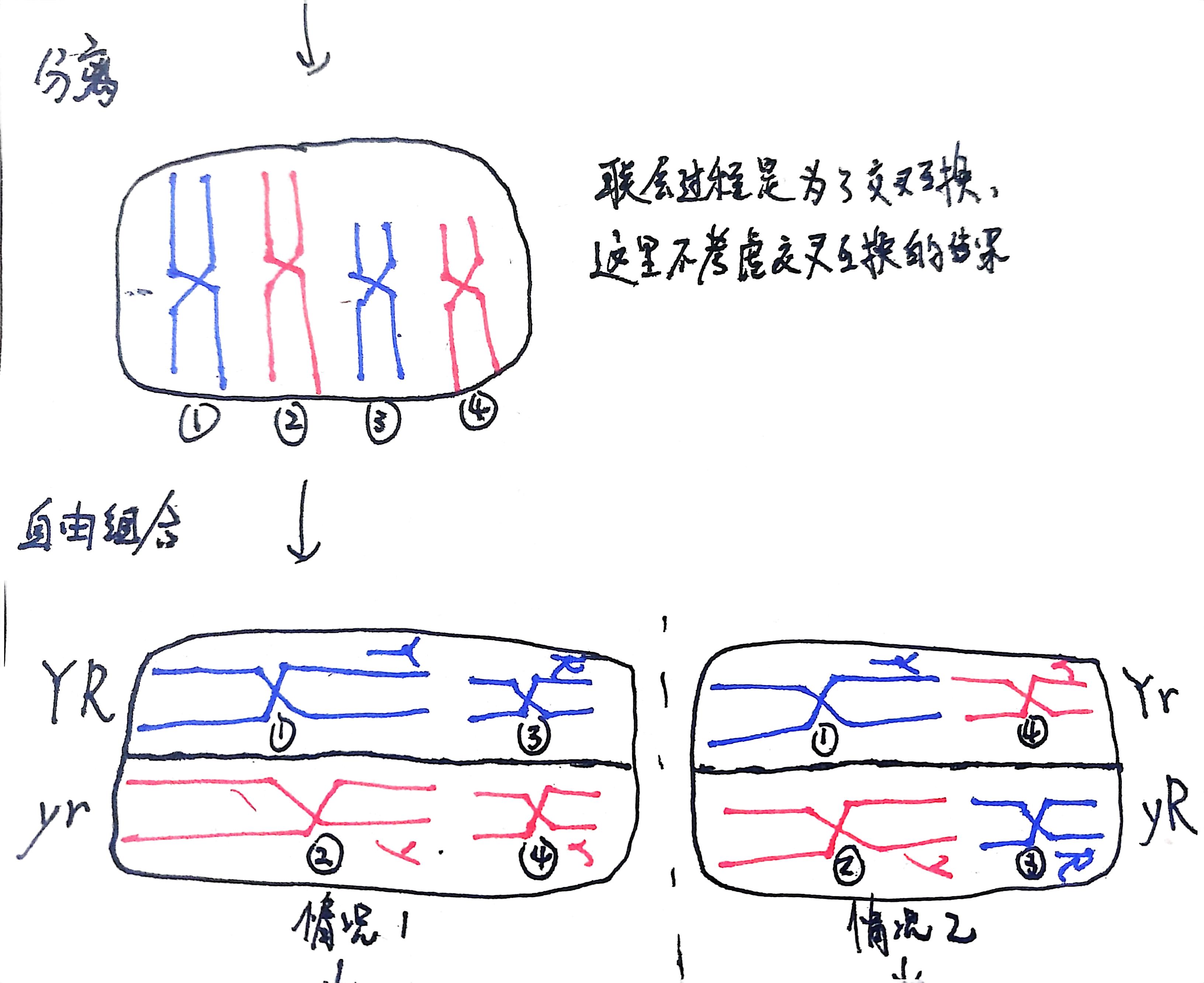
最后得到的次级精母细胞中染色体分别是 1 和 3;2 和 4(情况一),或者 1 和 4;2 和 3(情况二)
那为什么只有这 4 种组合可能呢?按照数学中的计算,4 个元素中能组成 2 个元素的集合一共有 6 种可能
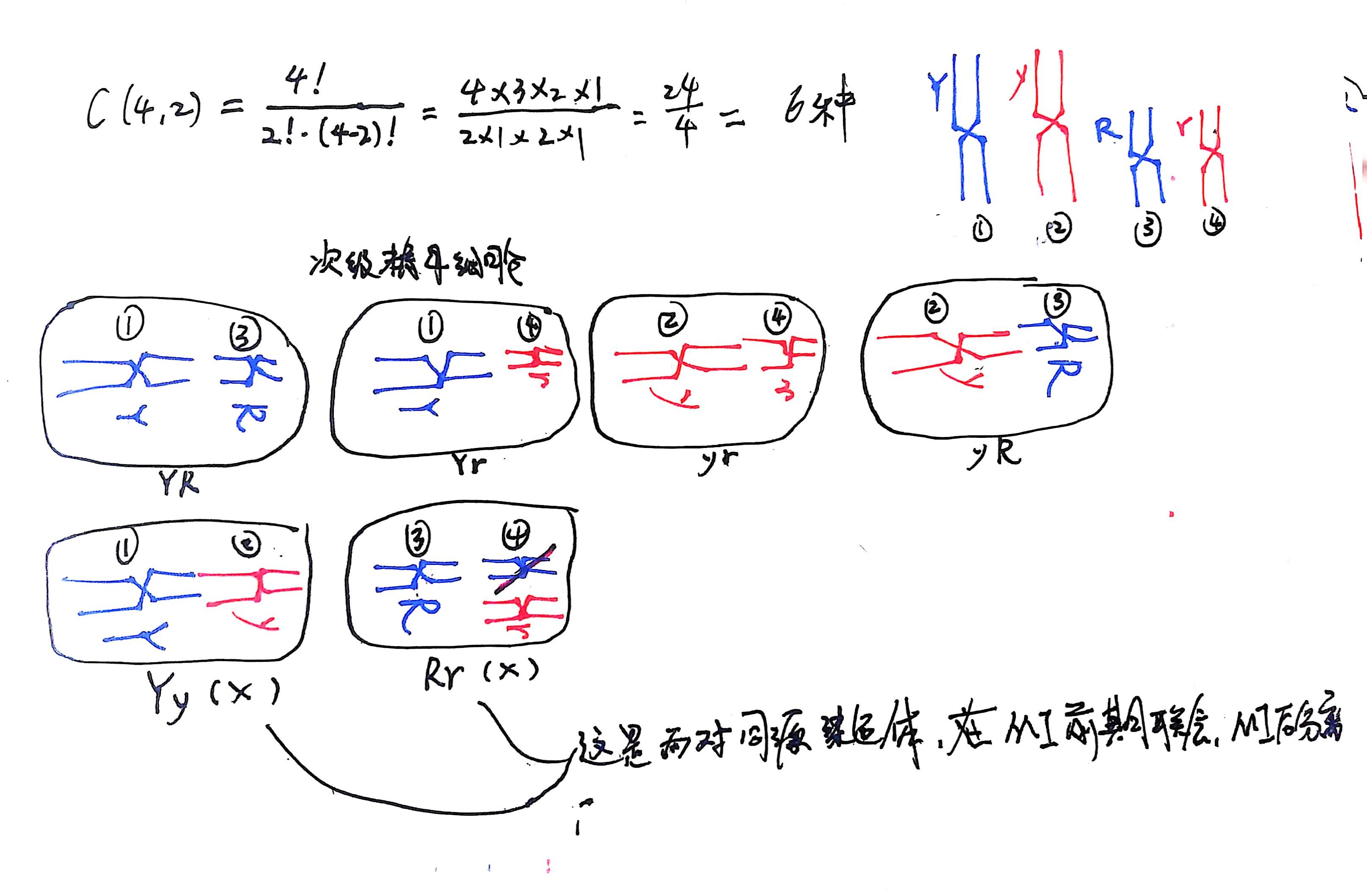
这就要再回顾一下刚才那句绕口的话了:在同源染色体上的等位基因彼此分离的同时,非同源染色体上的非等位基因自由组合
这句话中最重要的两个字就是 “同时”,同源染色体分离的同时,非同源染色体自由组合
也就是说 1 和 2 是一对同源染色体,1 与 2 刚分手后马上 1 就去找另一半,只能是 3 或 4,但不能再是 2 了
同时 2 也一样,分手后只能去找 3 或 4 但不能是 1;3 也一样,分手后只能去找 1 或 2 但不能是 4;4 也一样,分手后只能去找 1 或 2 但不能是3
注意我说的是 “只能” 、 “或” 这意味着强制的一对一组合,1 与 3 组合后 2 只能与 4 组合
所以最后的组合只有两种情况,一共四种组合:1 与 3,2 与 4 or 1 与 4,2 与 3
最后产生四种配子
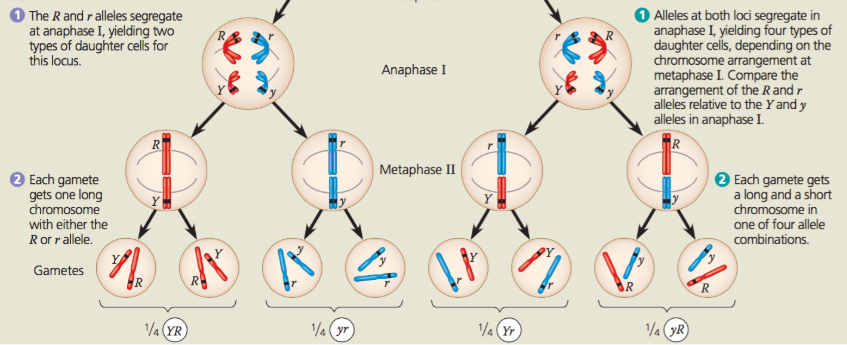
四种配子最后在旁氏表中一共有 16 种结合方式、9 种基因型、4 种表现型。
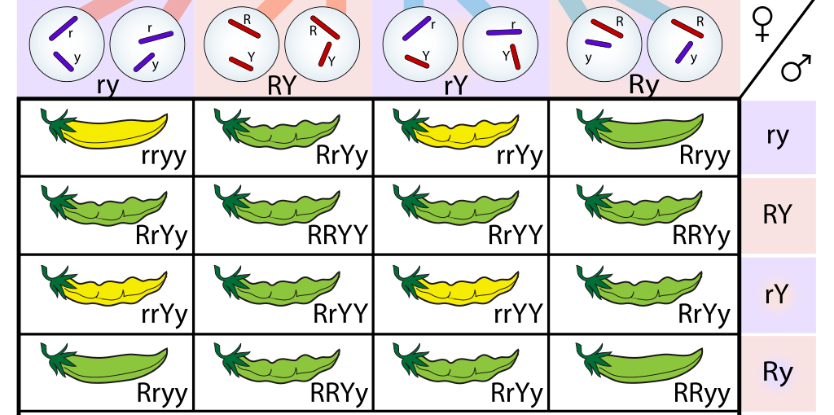
那么这里的形状表现就不能单单看显隐性了,而是四种性状比为 9:3:3:1(依赖基因的自由组合定律)
基因型的概率计算
如果要求 BbCc 自交基因型概率,当然可以画一张 16 格的旁氏表,那如果是求 AaBbCc 自交呢?以下默认是独立遗传且不考虑互换
基因与旁氏表关系
我们先来想想 AaBbCc 的旁氏表是多大,首先回顾一下配子的数目与什么有什么关系
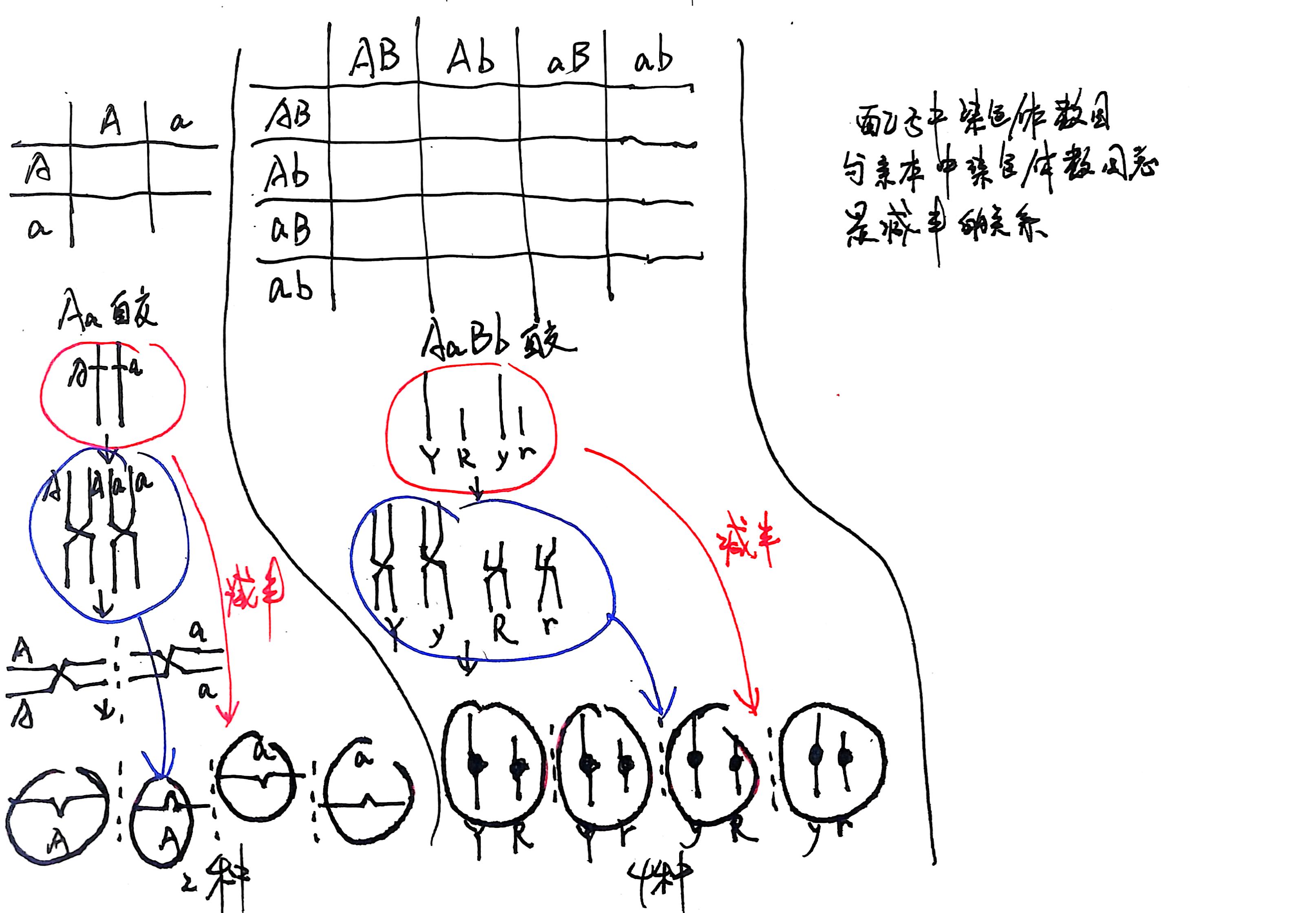
可以发现,配子的染色体与亲本相比减半,这是减数分裂导致的结果,但是我们还发现,配子的数目和亲本中染色体的数目竟然相同,这是结论吗?
当然不是,如果是 AA 作为亲本,亲本中有两条染色体,但是配子也只有 A 一种。
但是继续观察亲本染色体的种类就会发现
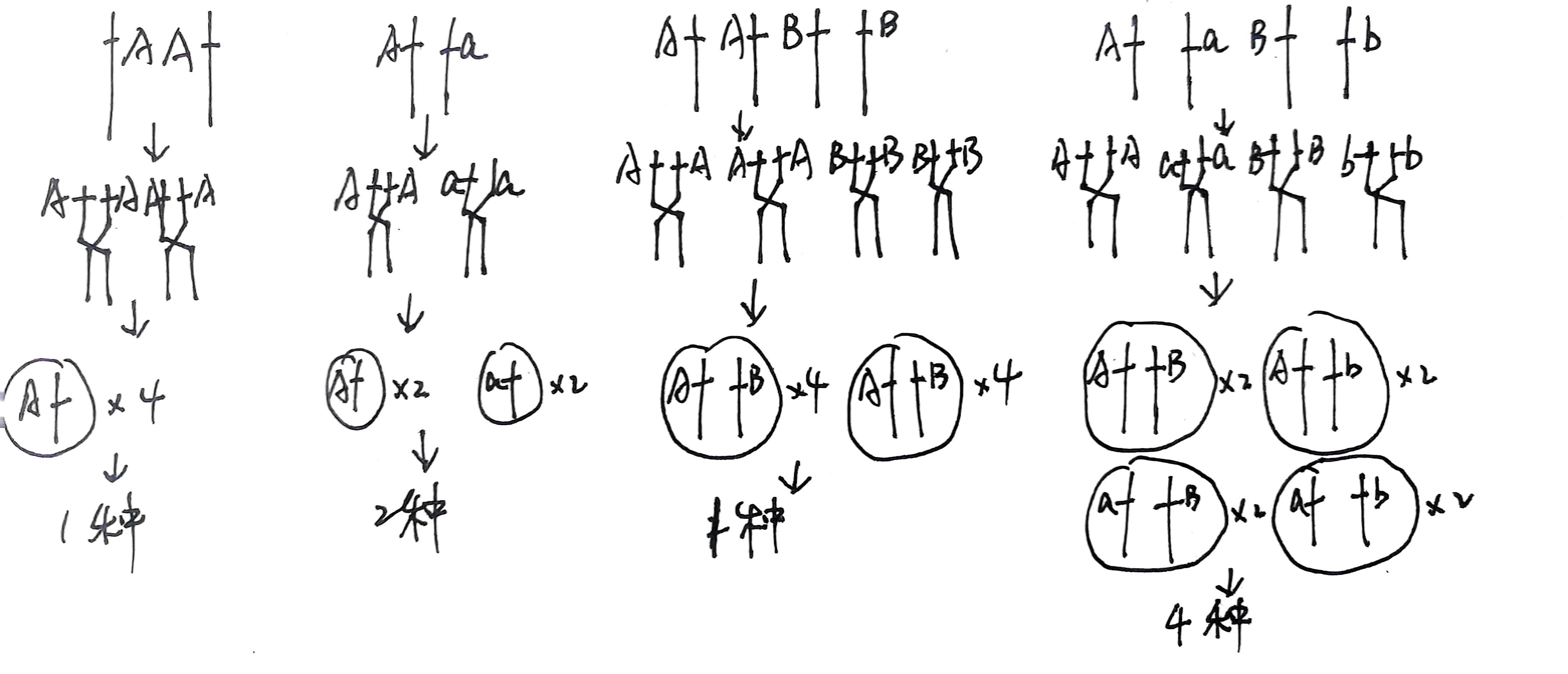
纯合亲本无论有几种染色体都只贡献一种配子,杂合亲本中,杂合基因的数量与配子数存在次方关系,具体体现在
| 基因型 | 杂合基因对数(n) | 配子种类数(2^n) | 配子类型 |
|---|---|---|---|
| AA | 0 | 1 | A |
| Aa | 1 | 2 | A、a |
| AABB | 0 | 1 | AB |
| AaBb | 2 | 4 | AB、Ab、aB、ab |
所以我们可以大胆猜测 AaBbCc 的配子应该有 8 种,所以自交的旁氏表应该有 64 格

从网上搜到的资料来看猜想正确,并且比例是 27:9:9:9:3:3:3:1
那如果是 AABbCCDdEEFfGg 呢?配子数和旁氏表又是多大?
不难看出 AABbCCDdEEFfGg 中有 4 组杂合子和 3 组纯合子,然后纯合子不影响配子数量,所以配子应该是 2^4 = 16 种, 旁氏表应该有 256 格
你可以通过下方的计算器来生成看看配子数量是否与你计算的一致
基因型自交计算器
基因型(例如: AaBb):
可能的配子:
旁氏表(Punnett Square):
| 配子 | AB | Ab | aB | ab |
|---|---|---|---|---|
| AB | AABB | AABb | AaBB | AaBb |
| Ab | AABb | AAbb | AaBb | Aabb |
| aB | AaBB | AaBb | aaBB | aaBb |
| ab | AaBb | Aabb | aaBb | aabb |
四方格旁氏表
继续回到我们开始的问题上,如果要求 BbCc 自交后子代基因型为 BbCc 的概率,当然可以画一张 16 格的旁氏表来求
但是画 16 格的旁氏表就已经很费时间了,所以可以利用四方格旁氏表来简化计算
在这种方法中,我们将整个问题分解成两个较小的问题,每个问题都与不同的遗传事件相关:
- 获得 Bb 基因型的概率是多少?
- 获得 Cc 基因型的概率是多少?
因为这两个问题都是独立事件,所以可以分别计算,然后利用乘法原理求解总概率。
如果你忘记了什么是独立事件,请跳转目录到乘法规则
抛硬币正面向上的概率是 1/2,并且抛硬币事件是独立事件,所以两次都是正面向上的概率是 1/2 * 1/2 = 1/4
获得 Bb 基因型的概率由 Bb 配子决定,很容易都能看出是 1/2,那么 Cc 同理也是 1/2。两个事件相乘,所以结果就是 1/2 * 1/2 = 1/4
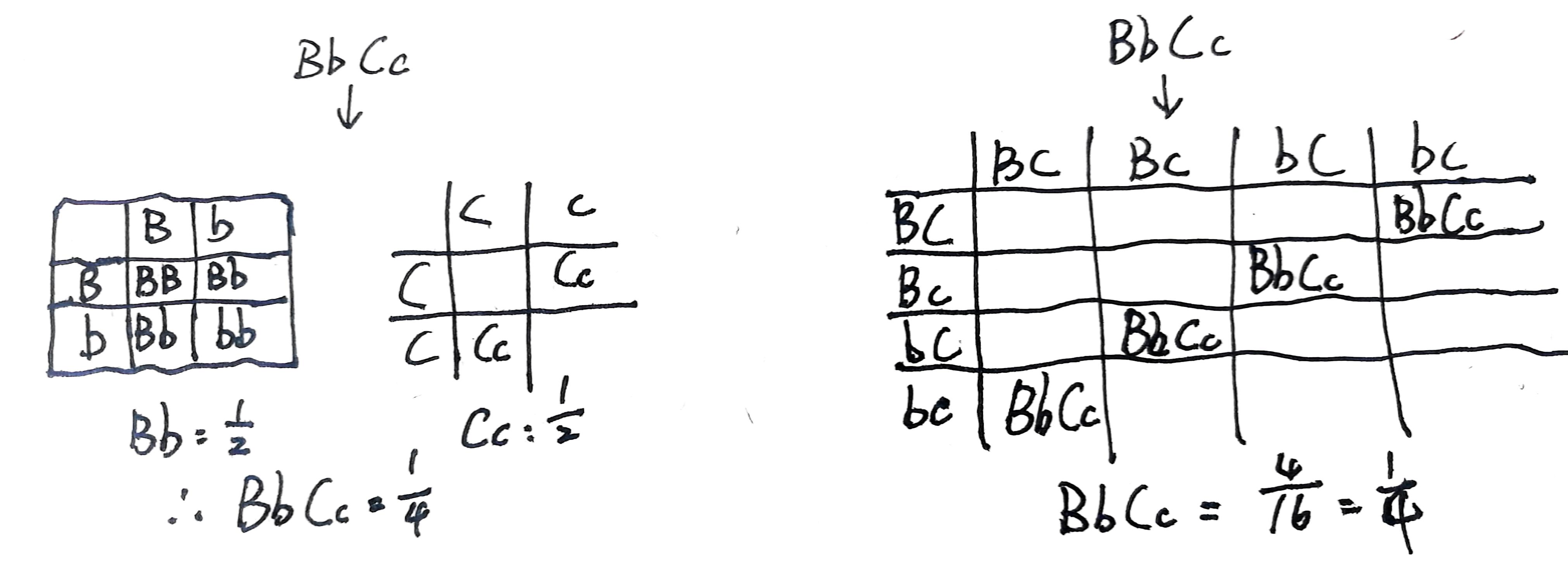
通过四方格旁氏表(左)和完整旁氏表(右)可以互相验证结果
选择适合你自己的方法
比如我现在需要求 AaBbCCdd x AabbCcDd 后代中显性比例
-
四方格旁氏表
如果用四方格旁氏表如图所示,需要分别求四个独立事件然后相乘
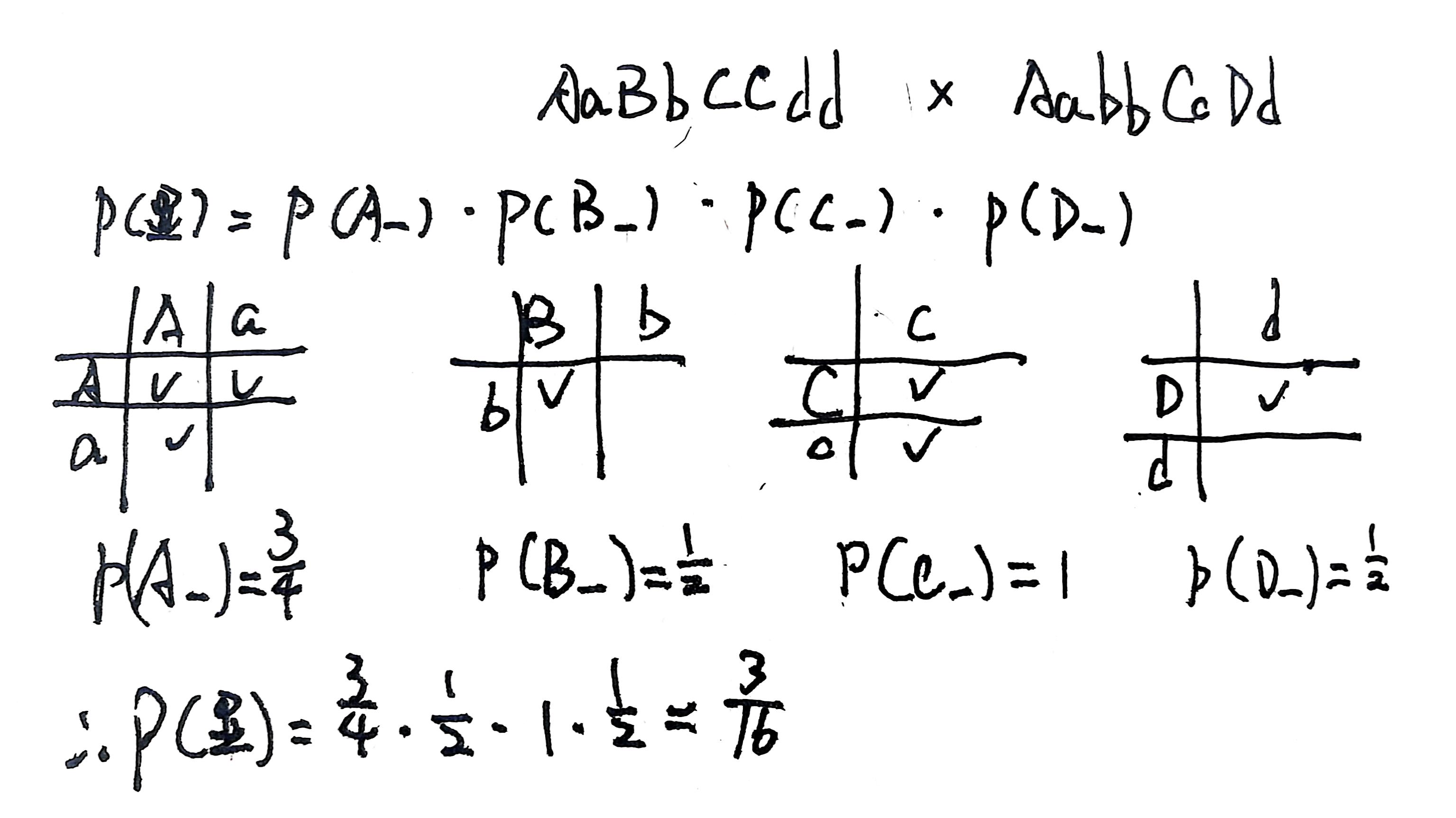
-
旁氏表法
我们已经知道了配子的计算公式,所以在用旁氏表法的时候,可以先算出表格的大小,然后再判断是用旁氏表还是用四方格旁氏表,当然一般都是四方格旁氏表更好算
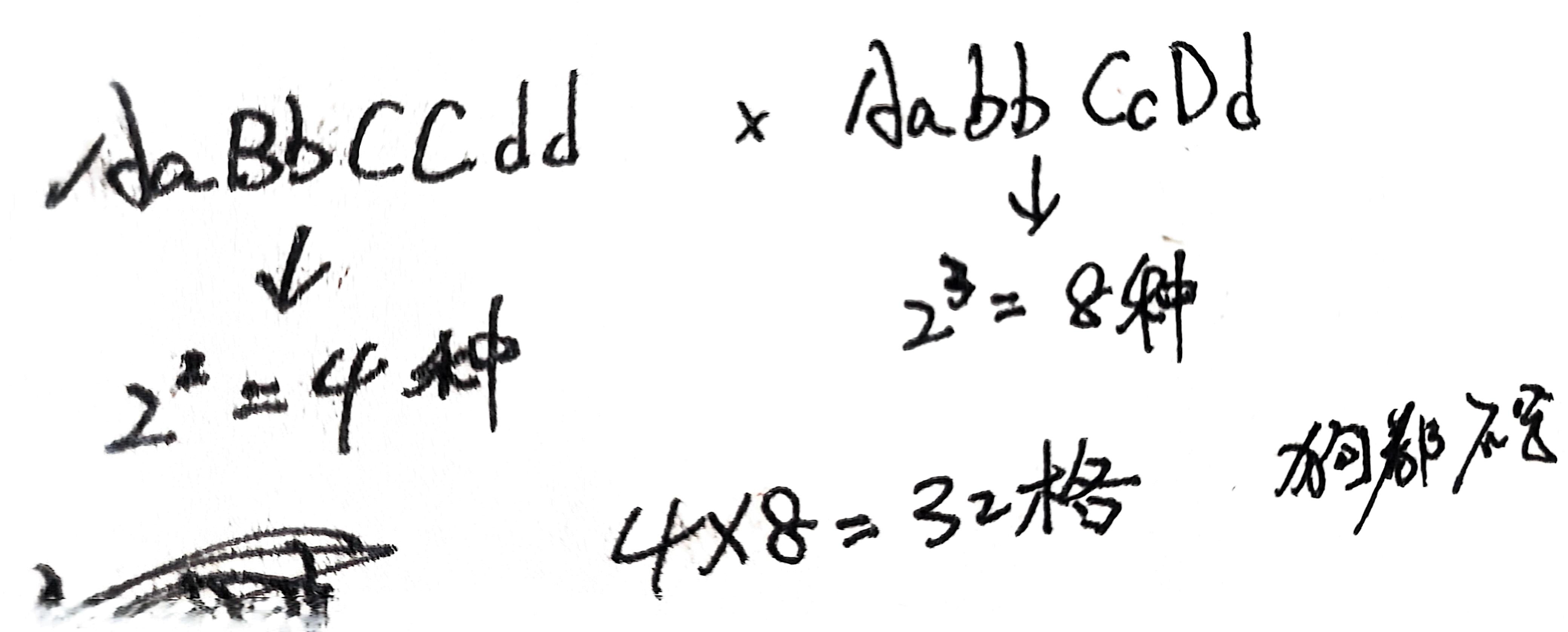
当然你可以用下面的杂交计算器来验证你的计算
基因型杂交计算器
亲本 1 可能的配子:
亲本 2 可能的配子:
旁氏表(Punnett Square):
| 配子 | AbCD | AbCd | AbcD | Abcd | abCD | abCd | abcD | abcd |
|---|---|---|---|---|---|---|---|---|
| ABCd | AABbCCDd | AABbCCdd | AABbCcDd | AABbCcdd | AaBbCCDd | AaBbCCdd | AaBbCcDd | AaBbCcdd |
| AbCd | AAbbCCDd | AAbbCCdd | AAbbCcDd | AAbbCcdd | AabbCCDd | AabbCCdd | AabbCcDd | AabbCcdd |
| aBCd | AaBbCCDd | AaBbCCdd | AaBbCcDd | AaBbCcdd | aaBbCCDd | aaBbCCdd | aaBbCcDd | aaBbCcdd |
| abCd | AabbCCDd | AabbCCdd | AabbCcDd | AabbCcdd | aabbCCDd | aabbCCdd | aabbCcDd | aabbCcdd |
不遵循独立遗传(连锁和交换定律)
生殖细胞形成过程中,位于同一染色体上的基因是连锁在一起,作为一个单位进行传递,称为连锁律。在生殖细胞形成时,一对同源染色体上的不同对等位基因之间可以发生交换,称为交换律或互换律
刚才的基因都是位于非同源染色体上的非等位基因,每一条染色体上只有一个基因,这些基因的分离和组合互不干扰,他们被称作独立遗传
独立遗传的基因遵循自由组合定律,因此自由组合定律也被称作独立分配定律,代表生物是豌豆
但后来发现有许多基因位于同一染色体上,这一现象称为基因连锁,代表生物是果蝇

染色体上足够靠近的基因会倾向于 “粘在一起”,而这些基因在染色体上往往会成对遗传,这种现象被称为遗传连锁
完全连锁
在极端情况下,决定种子颜色和形状的基因可能一直是成对遗传的。也就是说,黄色和圆形的等位基因可能一直在一起,绿色和皱褶的等位基因也可能一直在一起
更专业的来说就是指同一同源染色体上的两个非等位基因不会发生姐妹染色单体之间的交换
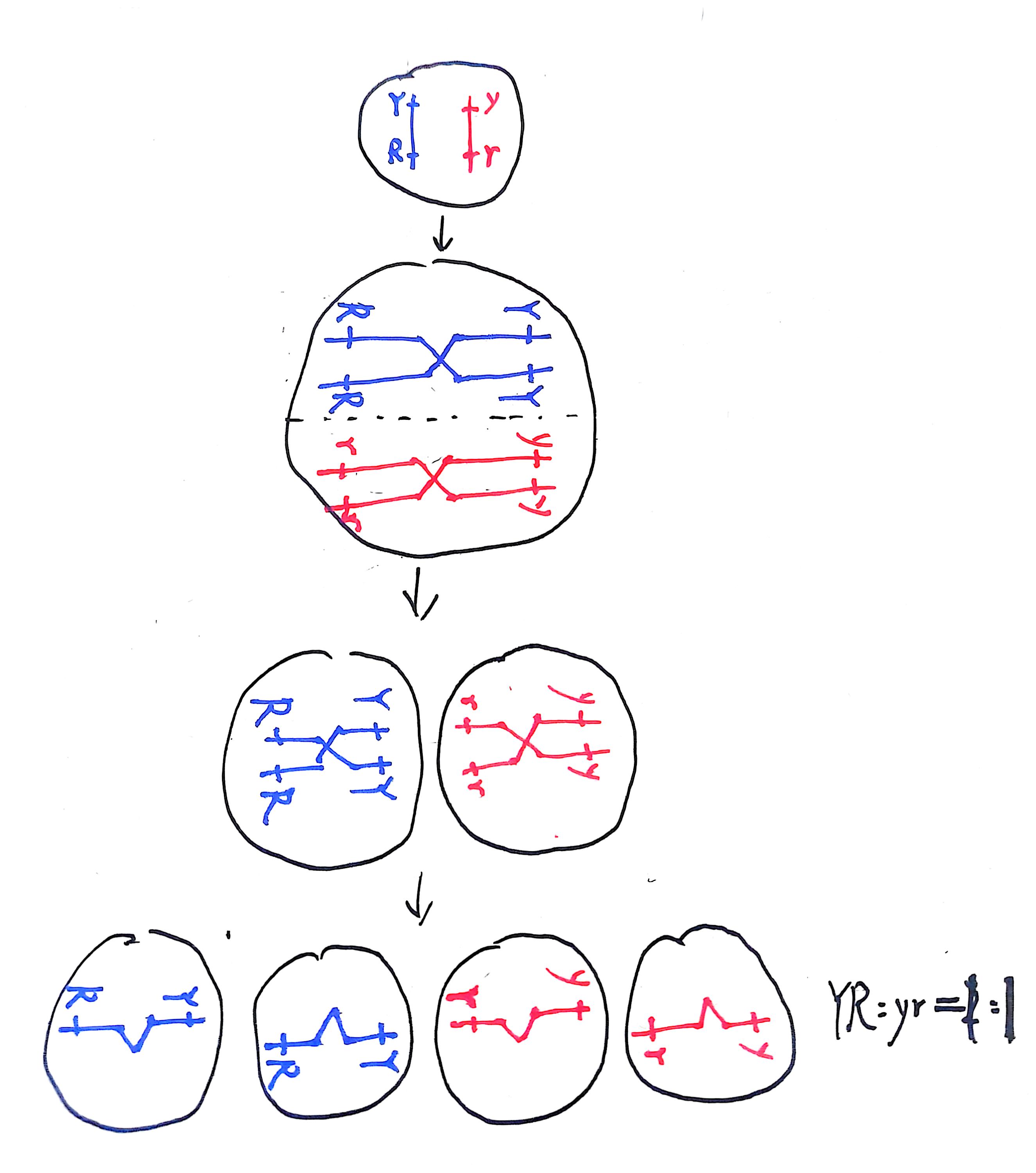
这种连锁双基因杂交只会为每个配子提供一个“组合单元”:一对 YR 等位基因或一对 yr 等位基因
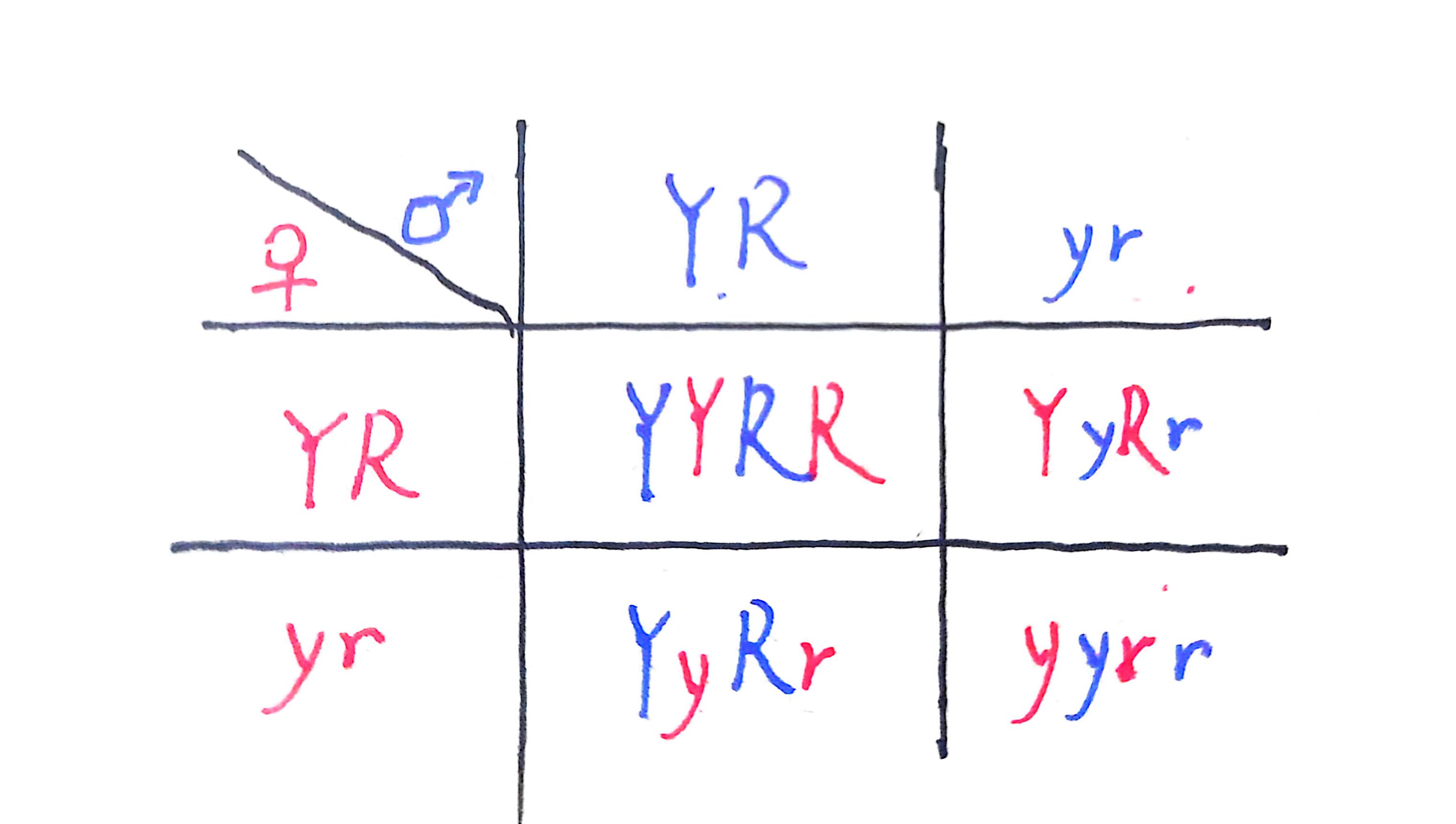
那么根据旁氏表计算可得显隐性之比为 3:1, 这与孟德尔的实际结果(9:3:3:1)大相径庭,不是独立遗传,不遵循自由组合定律
不连锁与交叉互换
当基因位于不同的染色体上或位于同一染色体上相距较远的地方时,它们会独立分配称为不连锁,符合孟德尔定律
注意即使基因位于同一条染色体上,但相距教远的基因也叫不连锁,此时也是独立遗传
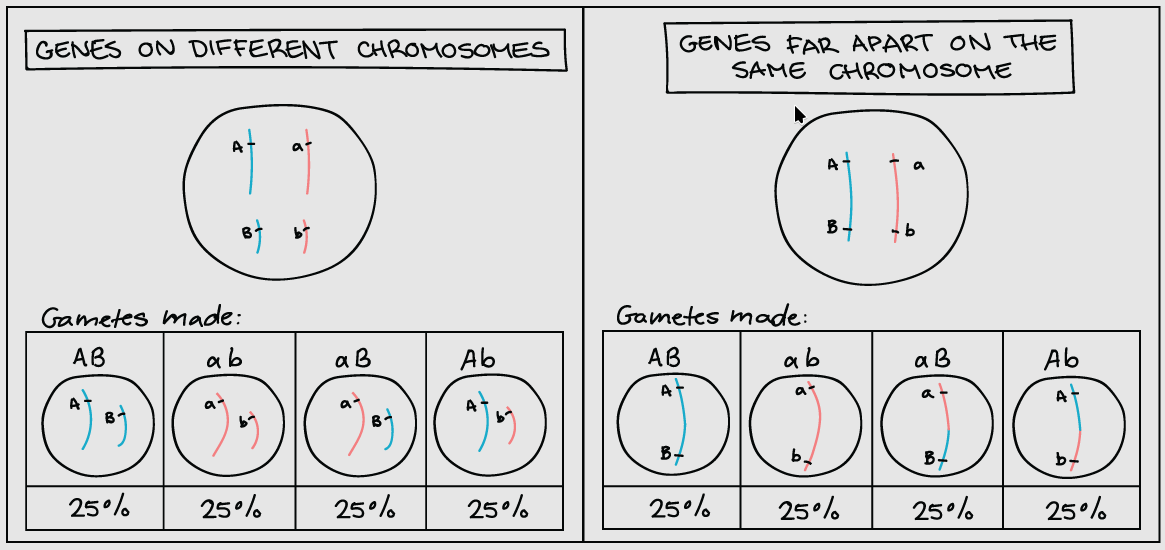
左图就是我们之前讨论的两对基因在不同染色体上独立遗传的情况,那么为什么右图也是独立的呢?
这里就要回顾一下之前的一个概念:交叉互换
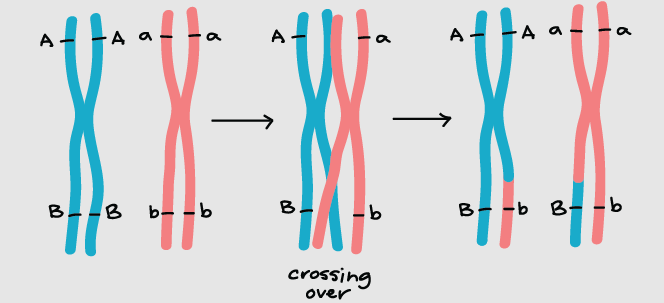
交叉互换指的是四分体中非姐妹染色单体之间的片段交换
先拿一对等位基因举例:

剩下的情况就不过多解释了,如果只研究一对等位基因,不管怎么换,都不会改变配子种类。但是 1 与 2 之间不能换,3 与 4 之间也不能换,因为他们是姐妹,交叉互换指的是非姐妹之间的片段交换
再看位于不同染色体上两对等位基因独立遗传的情况:
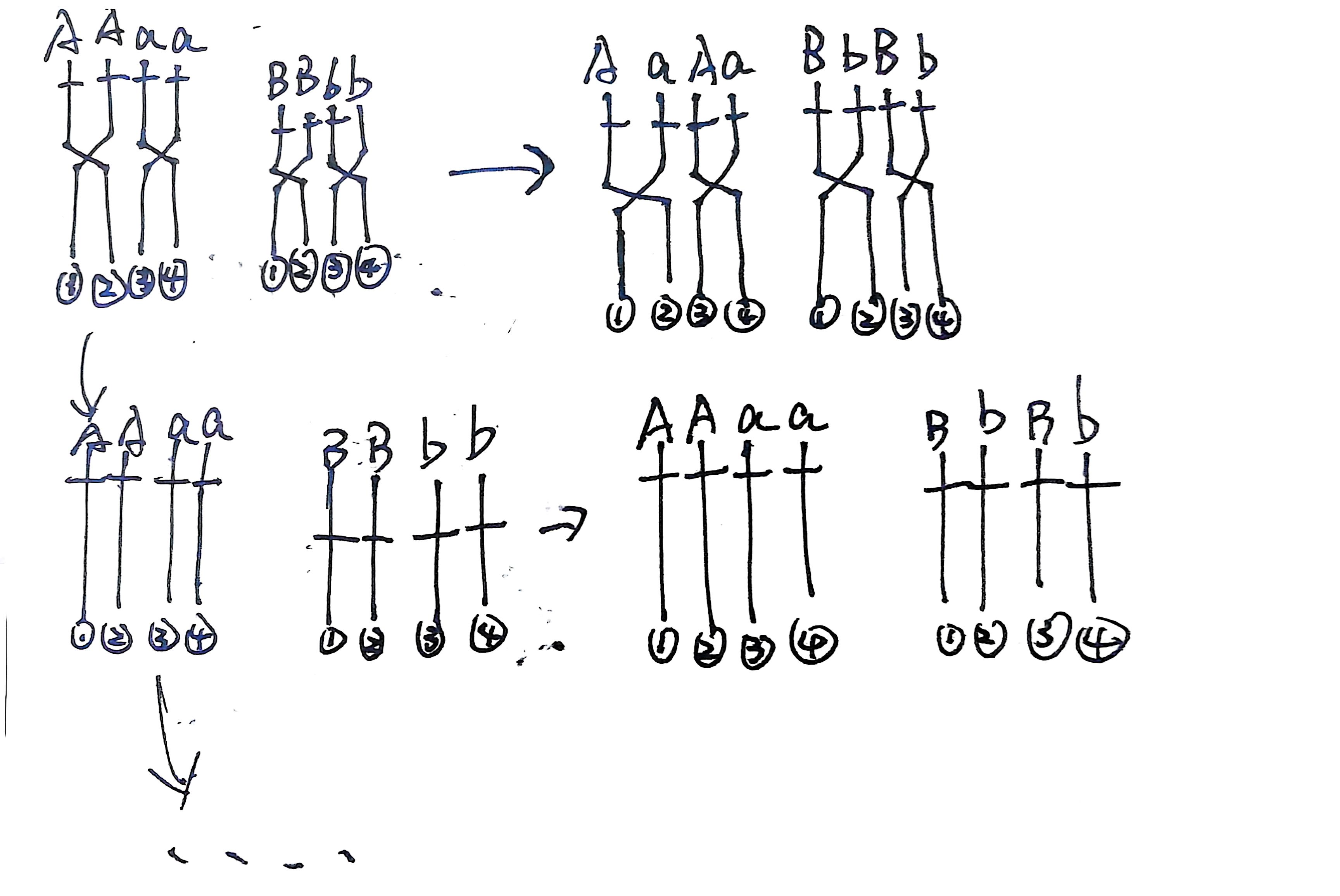
最后会发现和一对等位基因大差不差
最后看位于同一条染色体上两对等位基因独立遗传的情况
当基因位于同一条染色体上但相距甚远时,它们会通过交换(同源重组)独立地进行分配。当距离足够远时,以至于所有类型的配子都能够产生 25% 的频率,这种交换也是独立遗传,符合孟德尔的定律
那么符合孟德尔的定律的交换的流程应该如下:
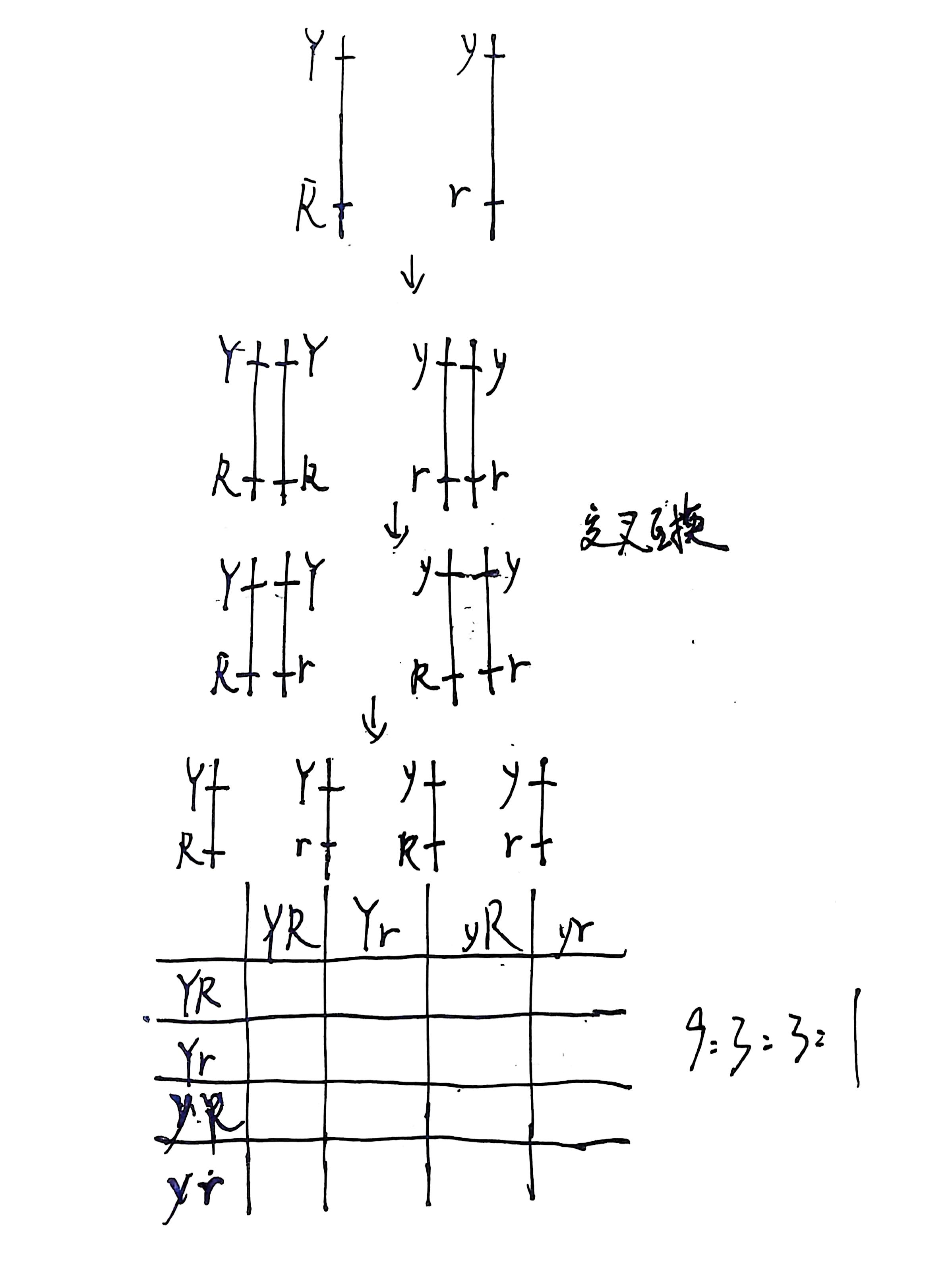
不完全连锁
当基因在同一染色体上非常接近时,交换仍然会发生,但结果(就产生的配子类型而言)会有所不同
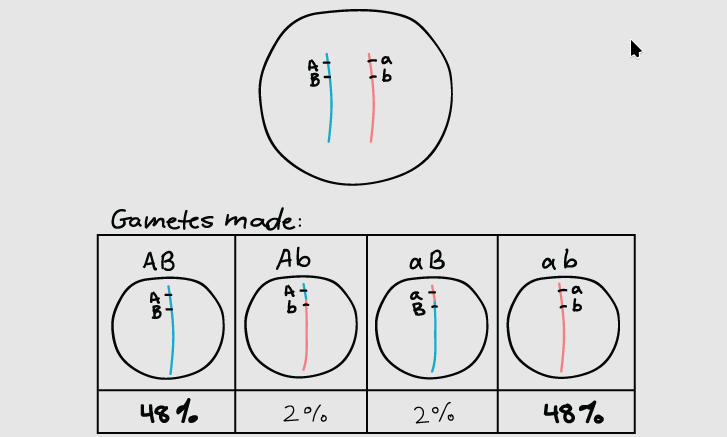
上图中较多的为原配型配子,而少量的为重组型配子。两个距离较近的基因之间发生交换的情况并不常见,所以重组配子类型非常罕见
由于这种关系,我们可以利用两个基因之间重组事件的频率(即它们的遗传连锁程度)来估计它们在染色体上的相对距离
综合性检验
实验设计题
某雌雄同株植物花的颜色由两对基因(A 和 a、B 和 b)控制,A 基因控制色素合成,AA 和 Aa 的效应相同;B 为修饰基因,淡化颜色的深度,BB 和 Bb 的效应不同
其基因型和表现型的对应关系见表,请回答下列问题:
| 基因型 | 表现型 |
|---|---|
| A_Bb | 粉色 |
| A_bb | 红色 |
| A_BB 或 aa__ | 白色 |
为研究两对基因(A 和 a、B 和 b)在一对染色体还是两对染色体时,某课题小组选用了基因型为 AaBb 的粉色植株进行探究,请设计实验:




将 AaBb 的粉色花自交后
a.若子代植株花色为 粉色:红色:白色 = 6:3:7,则两对基因可能在一对或两对同源染色体上,符合图中第一种和第二种类型;
如果不考虑交叉互换,粉色:红色:白色 = 6:3:7,则两对基因在两对同源染色体上独立遗传,符合图中第一种类型;
b.若子代植株花色为 粉色:白色 = 1:1,则两对基因在一对同源染色体上完全连锁,符合图中第二种类型;
c.若子代植株花色为 红色:粉色:白色 = 2:1:1,则两对基因在一对同源染色体上完全连锁,符合图中第三种类型。