ACM 算法入门培训第 01 讲 —— 基础数学

2025年 07月 22日

简体中文

你现在卡住的原因不是“不会写代码”，而是还没有建立算法竞赛的解题思维。先尝试独立暴力解题，从搞懂题意开始，逐步积累经验，然后再学习更高效的算法。ICPC 的核心是持续积累，现在开始就不晚。

导引问题：整数求和

给定一个正整数 $n$ ，求 $1 + 2 + 3 + ... + n$ 的结果，其中 $n <= 1,000,000,000$

高中的小伙伴都认识这是一道简单的数列求和，可以用循环逐个相加，或者用高斯公式直接计算。

迭代求和

先想一想，从 $1$ 一直累加到 $n$ ，这个过程是一种重复执行某个任务的控制结构，for 循环是最常见的迭代形式之一，适合在预先知道迭代次数时使用，代码如下：

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;

    // 初始化 s 为 0
    int s = 0;

    // 用循环求和
    for (int i = 1; i <= n; i++) {
        s += i;
    }

    cout << s << endl;
    return 0;
}

经过验证后程序正确：

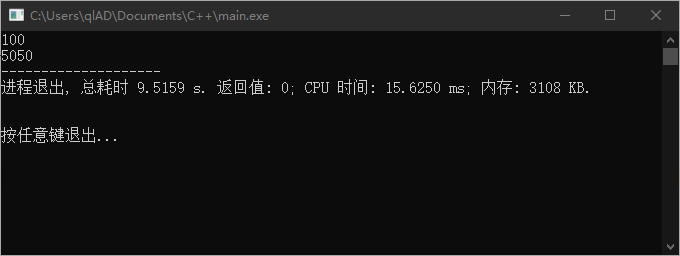
但是题目中 $n$ 最大可取 $1,000,000,000$ ，而 int 的最大值是 $2,147,483,647$ ，因此累加到最后 $s$ 的值会溢出。

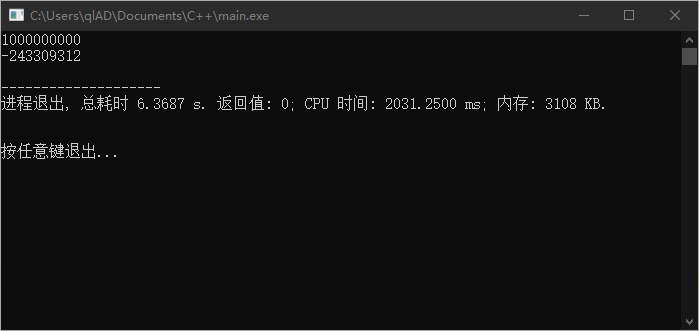
只需要将 $s$ 的类型换成 long long 即可

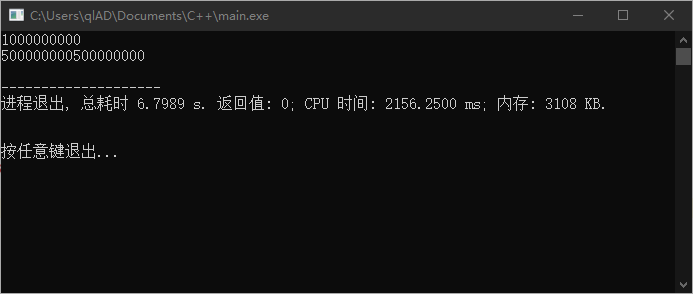
递归求和

递归是一种函数调用自身的编程技巧，适合处理具有重复结构的问题。

假设你的房间非常乱，书本、玩具、衣物等杂物到处都是。为了整理房间，你可以采用递归的方式：

基准情况：如果房间已经很干净，或者只剩下一个很小的区域需要整理（比如一个抽屉），那么直接整理这个区域，这就是递归的基准情况
递归情况：
- 先将房间划分为几个部分，比如书桌区域、床铺区域、地板区域
- 对每个区域分别进行整理。例如，整理书桌区域时，又可以把书桌划分为书架部分和桌面部分
- 每个部分的整理过程又可以进一步细分，直到达到基准情况（比如整理一个抽屉）
回溯：当你完成了一个区域的整理后，会回到上一级区域，继续整理下一个部分。比如，整理完书桌的书架部分后，再整理桌面部分，最后回到整个书桌区域，确认书桌整体是否已经整理好

现在我们要用递归来求和，可以将求和问题分解为更小的子问题，假设我们有一个求和函数为 sum(n)

当 $n=5$ 时，递归的过程如下：

调用 sum(5)，返回 5 + sum(4)
调用 sum(4)，返回 4 + sum(3)
调用 sum(3)，返回 3 + sum(2)
调用 sum(2)，返回 2 + sum(1)
调用 sum(1)，返回 1（基准情况）

回溯：

sum(2) 返回 2 + 1 = 3
sum(3) 返回 3 + 3 = 6
sum(4) 返回 4 + 6 = 10
sum(5) 返回 5 + 10 = 15

代码实现：

#include <iostream>
using namespace std;

int sum(int n) {
	// 基准情况：当 n 为 1 时，返回 1
	if (n == 1) {
		return 1;
	}
	// 递归情况：返回 n 加上从 1 到 n-1 的和
	return n + sum(n - 1);
}

int main() {
	int n;
	cin >> n;

	int s = sum(n);
	cout << s << endl;

	return 0;
}

但是递归的缺陷也很明显，当 $n$ 很大时，递归调用会导致栈溢出，程序崩溃。

你现在不用理解什么是栈

因此对于数据很大时，还是推荐使用迭代或者公式的方法

高斯公式

算法竞赛都会检查复杂度，也就是说代码不仅要正确，还要高效、简洁且易于理解。假设 $n = 1,000,000,000$ 时，用迭代的话循环次数太多会超出时间限制，用递归的话会导致栈溢出

一般对于求和问题，可以直接使用数学公式来优化，避免迭代或递归的开销

高斯公式： $sum = \frac{n(n + 1)}{2}$

#include <iostream>
using namespace std;

int main() {
	int n;
	cin >> n;

	// 初始化 s 为 0
	long long s = 0;

	// 用高斯公式求和
	res = n * (n + 1) / 2;

	cout << s << endl;
	return 0;
}

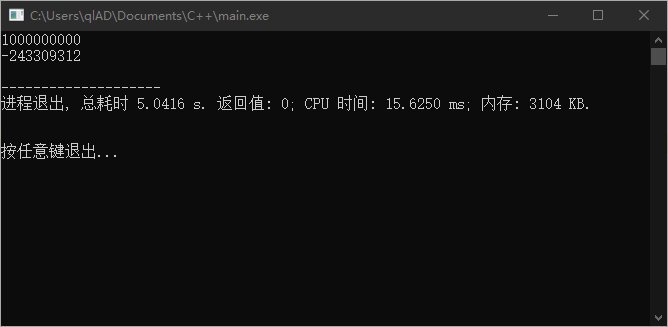
但是这样快是快，结果怎么不正确呢？ $n$ 在范围之内， $s$ 在范围之内，为什么算出来又爆了？

原因是高斯公式中有一步 $n(n + 1)$ ，当 $n = 1,000,000,000$ 时，这一步的结果超过了 int 的最大值，所以才爆

那么解决方法也很简单，给 $n$ 也换成 long long 就可以了

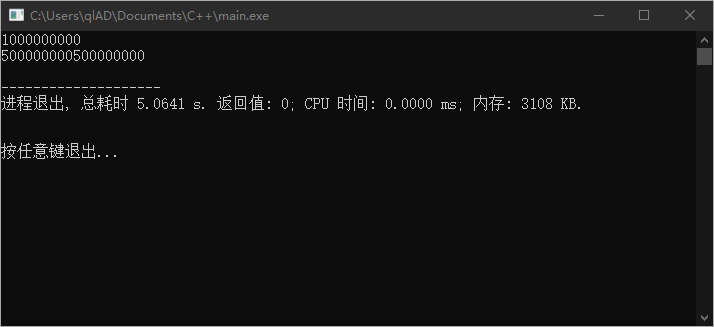
公式优化

当题目改成 $n <= 50000$ 时，这时候可以不用 long long，还有另一种处理数据溢出的方法

为什么不用 long long？虽然 long long 的性能开销很微小，但是还是大于 int，在算法竞赛中还是使用合适的数据类型好

即使 $n = 50000$ ，最后的答案也是 $1,250,025,000$ ，还没有超过 int 的最大值，但是公式中的 $n (n + 1)$ 这一步结果是 $2,500,050,000$ ，超过了 int 的最大值，这时候可以选择使用优化公式

我们先算除法，再算乘法时就不会让中间过程超 int

#include <iostream>
using namespace std;

int main() {
	int n;
	cin >> n;

	// 初始化 s 为 0
	int s = 0;

	// 用调整后的高斯公式求和
	s = n  / 2 * (n + 1);

	cout << s << endl;
	return 0;
}

但是这还不行，因为当 $n$ 是奇数时， $n / 2$ 结果是整数除法，结果会向下取整，导致结果不正确

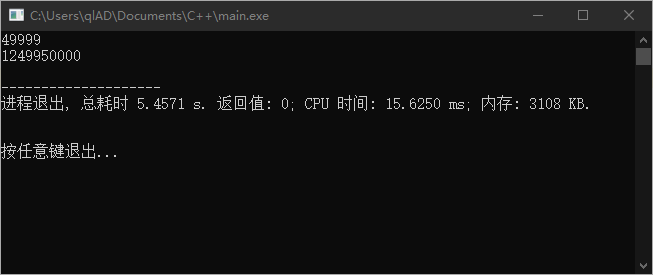
和正确结果的 $1,249,975,000$ 相比，少了很多

这时候只用把 $2$ 改成 $2.0$ 就行，这样就会变成浮点数除法，结果就会正确

如果你不用浮点数除法，也可以手动判断奇偶数， $n$ 和 $n+1$ 肯定是一奇一偶，先让偶数除以 $2$ 就可以了

#include <iostream>
using namespace std;

int main() {
	int n;
	cin >> n;

	// 手动处理奇偶性
	int s;
	if (n % 2 == 0) {
		// 如果 n 是偶数
		s = (n / 2) * (n + 1);
	} else {
		// 如果 n 是奇数
		s = (n + 1) / 2 * n;
	}

	cout << s << endl;
	return 0;
}

欧几里得算法

给定两个正整数 $a$ 和 $b$ ，求 $a$ 和 $b$ 的最小公倍数。

暴力枚举

比如要算 $10$ 和 $14$ 的最小公倍数（ $LCM$ ），我们可以从较大数 $14$ 到 $10 * 14$ 之间枚举，找到第一个能被 $10$ 和 $14$ 整除的数。

#include <iostream>
using namespace std;

int main() {
	int a = 10;
	int b = 14;

	int start = (a > b) ? a : b;   // 较大数
	int end   = a * b;             // 上界

	for (int lcm = start; lcm <= end; lcm++) {
		if (lcm % a == 0 && lcm % b == 0) {
			cout << lcm << endl;
			break;                 // 找到第一个就退出
		}
	}
	return 0;
}

需注意，如果 $a$ 和 $b$ 都很大，这种方法会非常慢。比如 $a$ 是一亿， $b$ 是一亿零一，枚举范围会非常大。

我们知道最小公倍数（ $LCM$ ）一定是较大数的整数倍，因此可以直接从较大数开始，每次增加较大数的值，直到找到一个同时能被 $a$ 和 $b$ 整除的数。

优化枚举方法：从最大数开始枚举，枚举范围为最大数的整数倍，那么此时只用判断能被最小值整除就行。并且在语法上，我们并不知道需要循环多少次，所以可以用 while 循环来代替 for

#include <iostream>
using namespace std;

int main() {
	int a, b;
	cin >> a >> b;

	int max = (a > b) ? a : b;
	int min = (a > b) ? b : a;
	int lcm = max;

	while (lcm % min != 0) {    // 不能整除就继续
		lcm += max;             // 每次加 max，只枚举其倍数
	}

	cout << lcm << endl;
	return 0;
}

辗转相除法

根据上文经验，有公式就用公式：

$LCM(a,b) = \frac{ab}{GCD(a,b)}$ 最小公倍数等于两数的乘积除以最大公约数。

由导引问题已经知道 $ab$ 可能会溢出，可以先除再乘，而且总能除尽，不用分奇数偶数的情况。

所以一般这个公式在编程中写成：

LCM(a, b) = a / GCD(a, b) * b

计算 $GCD$ 的方法可用辗转相除法，也称为欧几里得算法。

辗转相除法（欧几里德算法）的步骤：

用较大的数除以较小的数，得到余数
如果余数为 $0$ ，那么较小的数就是最大公约数
如果余数不为 $0$ ，则用余数去除之前的除数，得到新的余数
重复步骤 $2$ 和 $3$ ，直到余数为 $0$
最后的除数就是最大公约数

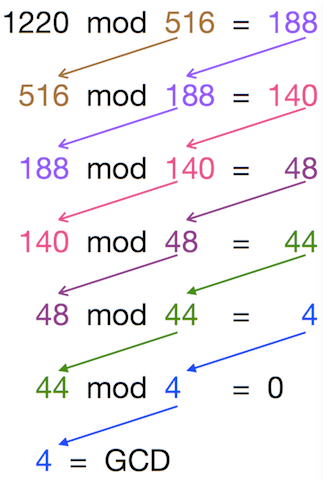
具体代码：

#include <iostream>
using namespace std;

// 计算最大公约数（GCD）
int gcd(int a, int b) {
	return b == 0 ? a : gcd(b, a % b);
}

// 计算最小公倍数（LCM）
int lcm(int a, int b) {
	return a / gcd(a, b) * b;
}

int main() {
	int a, b;
	cin >> a >> b;
	cout << lcm(a, b) << endl;

	return 0;
}

这里不用判断开始的两个数的大小：

gcd(14, 10) 正常流程。
gcd(10, 14) 第一步得到 gcd(14, 10)，正常流程。

还有如果题目中有范围，注意是否会溢出

找规律（循环节）

当遇到数据规模很大时的题目就不适合用暴力方法，基本思路应该是寻找规律

周期性规律

给定一个正整数 $n$ ，求 $n$ 个 $n$ 相乘的结果的个位数值（ $1 <= n <= 1,000,000,000$ ）

当 $n = 7$ 时， $7$ 的次方分别是 $7,49,343,2401,16807,117649,823543$ ，个位数分别是 $7,9,3,1,7,9,3$ ，所以答案应该是 $3$

当 $n = 8$ 时， $8$ 的次方分别是 $8,64,512,4096,32768,262144,2097152,16777216$ ，个位数分别是 $8,4,2,6,8,4,2,6$ ，所以答案应该是 $6$

可以明显看出个位数有某种周期关系，所以

先把 $n$ 换成它的个位数，然后观察 $n$ 的周期即可

n 的个位	连乘的个位规律	周期
2	2 → 4 → 8 → 6 → 2 …	4 次一循环
3	3 → 9 → 7 → 1 → 3 …	4 次一循环
4	4 → 6 → 4 → 6 …	2 次一循环
0,1,5,6	永远不变	1 次
7	7 → 9 → 3 → 1 → 7 …	4 次
8	8 → 4 → 2 → 6 → 8 …	4 次
9	9 → 1 → 9 → 1 …	2 次

并且还会发现大数次方的个位数的周期和个位数次方的个位数次方的周期是一样的，我不知道怎么解释，如下图：

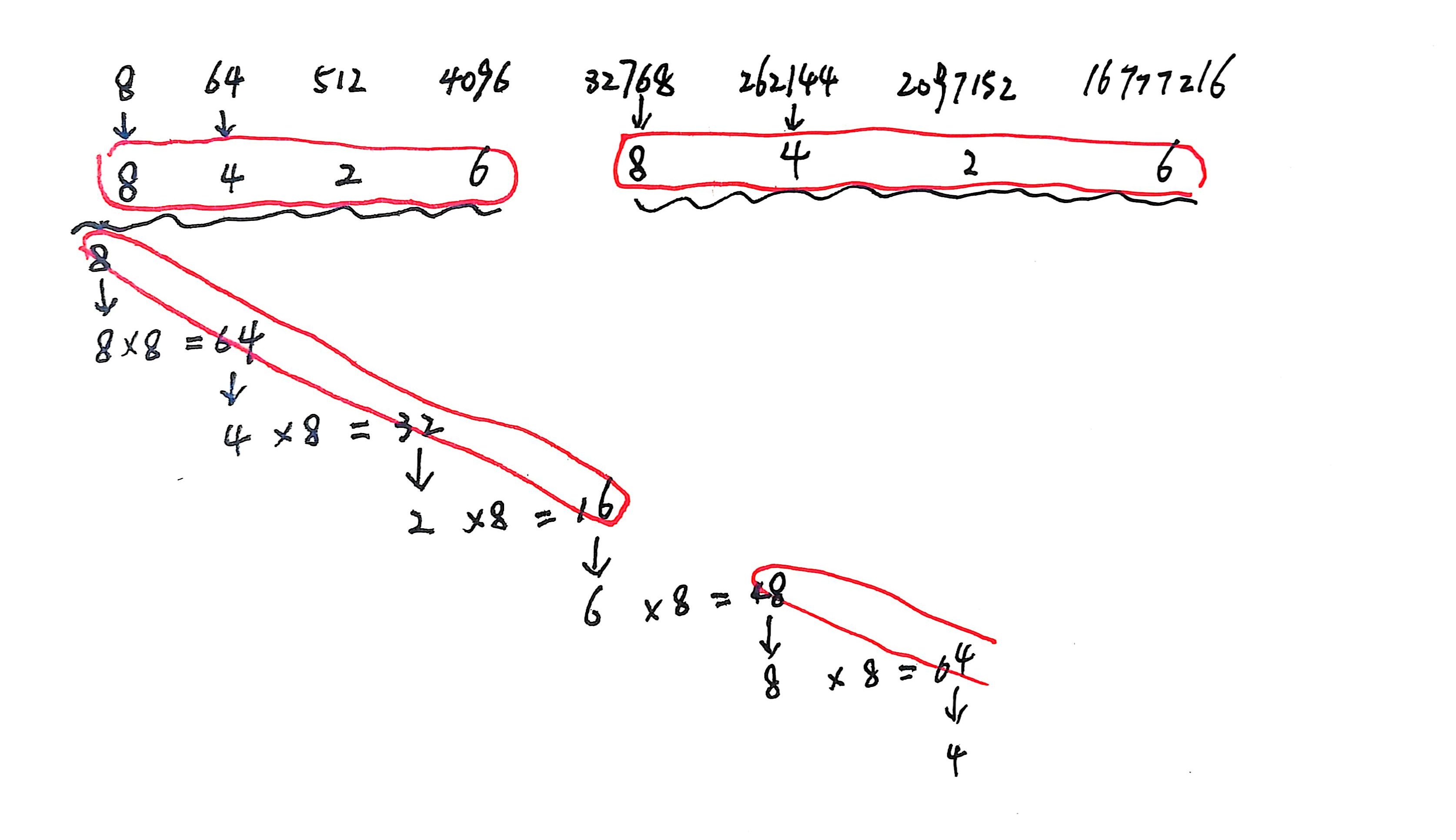
做法：

先把 $n$ 的个位数 $d$ 取出来。
如果 $d$ 是 $0/1/5/6$ （周期为 $1$ ），答案就是 $d$
否则，计算 $n$ 在周期内的位置，即 $pos = n \% p$
根据 $pos$ 的值，确定 $n^n$ 的个位数

代码实现：

#include <iostream>
using namespace std;

int last_digit_pow(int n) {
	// 1. 提取 n 的个位数
	int d = n % 10;

	// 2. 各数字的周期长度
	int period[10] = {1, 1, 4, 4, 2, 1, 1, 4, 4, 2};

	// 3. 特殊情况：周期为 1 的个位数
	if (d == 0 || d == 1 || d == 5 || d == 6) {
		return d;
	}

	// 4. 计算 n 在周期内的位置
	int p = period[d];
	int pos = n % p;
	if (pos == 0) {
		pos = p;  // 如果 pos 为 0，调整为周期的最后一个位置
	}

	// 5. 计算 d^pos 的个位数
	int res = 1;
	for (int i = 0; i < pos; ++i) {
		res = (res * d) % 10;
	}
	return res;
}

int main() {
	int n;
	cin >> n;
	cout << last_digit_pow(n) << endl;
	return 0;
}

这种方法利用了个位数的周期性规律，避免了直接计算大数的幂次方，从而非常高效。

斐波那契数列

有一种斐波那契数列，定义如下：

$F(0) = 7, F(1) = 11$

$F(n) = F(n-1) + F(n-2) (n >= 2)$

给定一个 $n(n <= 1,000,000)$ ，判断 $F(n)$ 能否被 $3$ 整除

这里我们只关心 $F(n)\%3$ 是否为 $0$ ，根据递推式：

$F(n)\%3 = (F(n-1) + F(n-2))\%3 = (F(n-1)\%3 + F(n-2)\%3)\%3$

即所求的值为前两项对 $3$ 取模的和再对 $3$ 取模

所以可以直接写出前几项：

$7 \% 3 = 1$

$11 \% 3 = 2$

$(1\%3+2\%3)\%3 = 0$

则前几项的 $F(n) \% 3$ 为：

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
F(n) mod 3	1	2	0	2	2	1	0	1	1	2	0	2	2	1	0	1

可以看出第 $n$ 项对 $3$ 取模的结果是周期性的，周期为 $8$ ，取模结果是 $1,2,0,2,2,1,0,1$ 然后重复

所以可以直接用 n mod 8 来判断，当前仅当 n mod 8 为 $2$ 或 $6$ 时， $F(n)$ 能被 $3$ 整除

#include <iostream>
using namespace std;

int main() {
    int n;
    while (cin >> n) {
        int r = n % 8;
        if (r == 2 || r == 6) {
            cout << "yes" << endl;
        } else {
            cout << "no" << endl;
        }
    }
    return 0;
}

模运算的性质

在快速幂的题目中常常有模运算一起考察，包括上文中用到了两个模运算的性质，希望尽快熟悉它们

基本运算：

$(a+b)\%p=(a\%p+b\%p)\%p$
$(a-b)\%p=(a\%p-b\%p)\%p$
$(a*b)\%p=(a\%p * b\%p)\%p$
$a^b\%p=((a\%p)^b)\%p$

结合律：

$((a+b)\%p+c)\%p=(a+(b+c)\%p)\%p$
$((a*b)\%p * c)\%p= (a * (b*c)\%p)\%p$

交换律：

$(a+b)\%p=(b+a)\%p$
$(a*b)\%p=(b*a)\%p$

分配律：

$(a+b)\%p=(a\%p+b\%p)\%p$
$((a+b)\%p*c)\%p = ((a*c)\%p + (b*c)\%p\ )\%p$

快速幂运算

假如用暴力求 $123^{456}$ 则需要进行 $455$ 次运算，但是对算式进行变形 $(123^{2})^{228}$ 则减少成了 $228$ 次运算

所以继续变形，奇数时多乘一个（会向下取整），偶数时继续做类似处理

递归实现：

int power(int a, int n) {
	if (n == 0) {
		return 1;  // 基准情况：任何数的 0 次方为 1
	} else {
		int temp = power(a * a, n / 2);  // 递归调用，计算 (a^2)^(n/2)
		if (n % 2 == 1) {
			temp *= a;  // 如果 n 是奇数，额外乘以一个 a
		}
		return temp;  // 返回最终结果
	}
}

迭代实现：

int power(int a, int n) {
	int result = 1;  // 初始化结果为1
	while (n > 0) {
		if (n % 2 == 1) {  // 如果n是奇数
			result *= a;  // 将a乘到结果中
		}
		a = a * a;  // 将a平方
		n = n / 2;  // 将n减半
	}
	return result;
}

求 $A^B$ 的最后三位数 $(1 <= A,B <= 100000000)$

快速幂运算一般不会直接求 $A^B$ ，而是对结果进行取模运算

#include <iostream>
using namespace std;

int power_mod(int a, int b, int mod) {
	int result = 1;  // 初始化结果为1
	a = a % mod;     // 首先对底数取模
	while (b > 0) {
		if (b % 2 == 1) {  // 如果b是奇数
			result = (result * a) % mod;  // 将a乘到结果中，并取模
		}
		a = (a * a) % mod;  // 将a平方，并取模
		b = b / 2;  // 将b减半
	}
	return result;
}

int main() {
	int A, B;
	cin >> A >> B;
	cout << power_mod(A, B, 1000) << endl;
	return 0;
}

二分查找

二分查找是一个很普遍的算法，在字典里，每个汉字都对应一个拼音，而字典是按照拼音字母顺序排列的。

假设我们需要查找一个拼音首字母为 $r$ 的字，通常会按照以下步骤实现：

翻开字典约一半的页数，查看该页的首字母是什么，假设首字母为 $m$
由于在拼音字母表中 $r$ 位于 $m$ 之后，所以排除字典前半部分，查找范围缩小到后半部分
不断重复步骤 $1$ 和步骤 $2$ ，直至找到拼音首字母为 $r$ 的页码为止

查字典这个小学生必备技能，实际上就是著名的“二分查找”算法

但是二分查找的前提是数据的单调性，比如字典拼音是按顺序排列的

有 $N$ 个人（ $1<=N<=50$ ）按照从矮到高左右排列，这时候又来了一个人，请你确定这个人的位置

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N, X;
	cin >> N;
	vector<int> H(N);
	for (int i = 0; i < N; ++i) cin >> H[i];
	cin >> X;

	int left = 0, right = N - 1;
	while (left <= right) {
		int mid = left + (right - left) / 2;
		if (H[mid] < X) {
			left = mid + 1;
		} else {
			right = mid - 1;
		}
	}

	cout << left + 1 << endl;
	return 0;
}

三分查找

在区间内用两个变量将区间分成三份，这样的查找算法称为三分查找，也就是三分法。

三分法常用于求解单峰函数的最值。

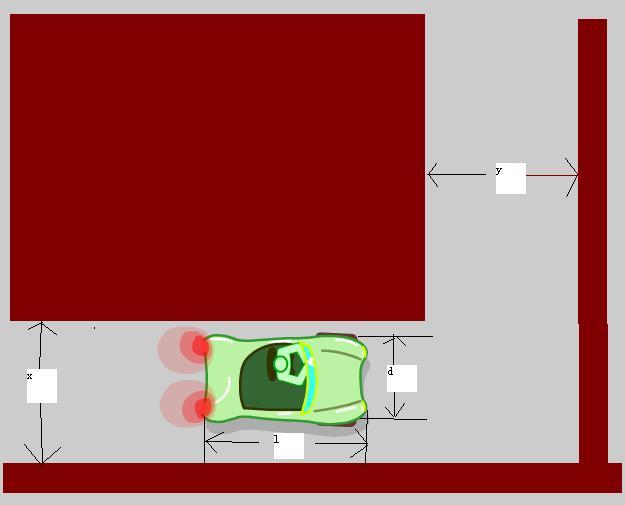
给定一个转角两端的宽度X, Y，以及汽车的长度和宽度L, D，判断汽车能否转过这个角（理想化转角）

题目传送门

#include <cmath>
#include <iostream>
#include <iomanip> // 用于设置小数精度
using namespace std;

const double eps = 1e-6;
const double pi = acos(-1.0);

// 定义函数 fun，计算在角度 i 时汽车在转角处的宽度需求
double fun(double i, double x, double l, double d) {
    return (x - l * sin(i) - d / cos(i)) / tan(i);
}

// 三分法函数，用于寻找函数 fun 的最小值
double ternary_search(double x, double y, double l, double d) {
    double ll = 0, rr = pi / 2;
    while (rr - ll > eps) {
        double midl = (2 * ll + rr) / 3;
        double midr = (ll + 2 * rr) / 3;
        if (fun(midl, x, l, d) < fun(midr, x, l, d)) {
            rr = midr;
        } else {
            ll = midl;
        }
    }
    return fun(ll, x, l, d); // 返回最小值
}

int main() {
    double x, y, l, d;

    // 输入循环
    while (cin >> x >> y >> l >> d) {
        // 输入验证
        if (x <= 0 || y <= 0 || l <= 0 || d <= 0) {
            cout << "输入数据无效，请确保所有输入值均为正数。" << endl;
            continue;
        }

        // 使用三分法计算最小宽度需求
        double min_width_req = ternary_search(x, y, l, d);

        // 判断汽车是否可以通过转角
        if (min_width_req > -y) {
            cout << "yes" << endl;
        } else {
            cout << "no" << endl;
        }
    }

    return 0;
}

文章分类在笔记

#ACM #算法入门 #基础数学